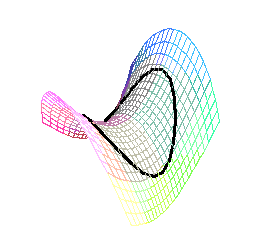sphericon 2 The Differential Geometry of the Sphericon
2. An insider's guide to surface curvature and geodesics
Curvature: If you are a two-dimensional creature living on a smooth surface you feel its curvature in your guts. When you go from a flat region to one of positive curvature your insides get stretched with respect to your periphery; if you enter a region of negative curvature they get compressed.
For example, suppose you are a disc of radius 1 living on the flat part of the surface, so your circumference is 2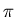 = 6.28.. and your area is
= 6.28.. and your area is 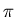 = 3.14.
= 3.14.
- Positive:

| Suppose part of the surface is curved like the graph of z= -(x2+y2) (this graph has positive curvature). If you slide over there so that the middle of your body is at (0,0,0), your perimeter will fit exactly on the circle at height -1, but your area will have been stretched to 5.33.. units. |
- Negative:
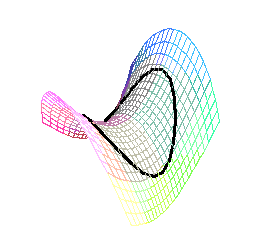
| On the other hand suppose part of your surface is curved like the graph of z=x2-y2 (this graph has negative curvature). If the middle of your body is at the point (0,0,0), your perimeter will fit the circle in the graph that lies over the circle r=.715.. in the plane; your insides will have to fit in the enclosed area which is only 2.26.. units. |
| |
Geodesics: The geographers in your two-dimensional universe need to be able to locate and measure areas of non-zero curvature without risking their insides. They may have discovered a theorem due to Gauss which permits these measurements. This theorem is stated in terms of geodesics. These are the paths on the surface which are as straight as possible: they turn neither to the left nor to the right, and their only bending is that which is forced on them by following the surface.
- If the surface is an ordinary plane, the geodesics are ordinary straight lines.
- If the plane is bent without stretching into a cylinder or a cone, the lines remain geodesics, even though they may bend with the plane.
- On a sphere the geodesics are great circles. If you travel along the equator or along a meridian line, you always move straight ahead. If you travel along a latitude which is not the equator (think of one very near the North Pole) you have to keep turning to stay on the line. Such a latitude is not a geodesic.
On to Sphericon page 3.
Back to Sphericon page 1.



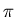 = 6.28.. and your area is
= 6.28.. and your area is