The Shadow Knows: How to measure time with a sundial

In this article, we'll consider some mathematical issues involved in constructing a sundial...

David AustinDavid Austin
Grand Valley State University
Email David Austin

Email to a friendMail to a friend Print this articlePrint this article

Introduction

As young children, we learn to note the passing of time by observing the sun's location in the sky or the lengthening of shadows cast by the sun. Long ago, people discovered that this observation may be used to create systems to accurately measure time; the ancient Egyptians were the first people that we know who made systematic efforts to keep time using the sun. Though time is now defined in terms of a specific atomic process, the heliochronometer, an instrument that indicates time through the location of the sun's shadow, was used to keep time in French train stations until as recently as the early 1900s.

In this article, we'll consider some mathematical issues involved in constructing a sundial. Today, sundials are usually seen as decorative accents in gardens or more prominently as public works of art. With care, however, it is straightforward to create sundials that are accurate to within a minute. We'll see that the process of constructing a dial involves some simple applications of three-dimensional geometry that help us translate the sun's motion across the sky into an understanding of how a shadow will move across the sundial's table.

The motion of the sun

In simplest terms, the task of constructing a sundial requires us to relate the sun's position in the sky to the position of a shadow it casts on some surface. Let's begin by recalling the processes that regulate the sun's position in the sky, focusing on the most important features and ignoring some more subtle issues.

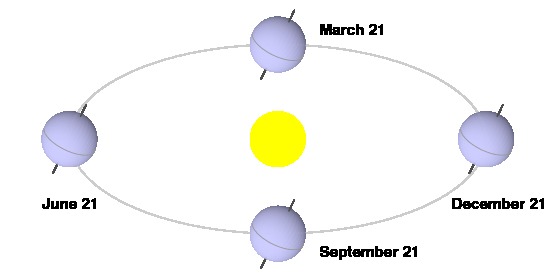
First, recall that the earth rotates on its axis once every 24 hours, which defines a day, and that the earth revolves around the sun once a year, which defines a year.

 

Looking a little more closely, we see there is some interaction between these two types of motion. Our usual notion of a day is the solar day, the length of time between when the sun appears at the same point in the sky, perhaps due south of our location when viewing from the northern hemisphere. This is the length of a day as measured by a sundial. (In this image, the distance traveled by the earth along its orbit in one day is exaggerated for the sake of clarity.)

 

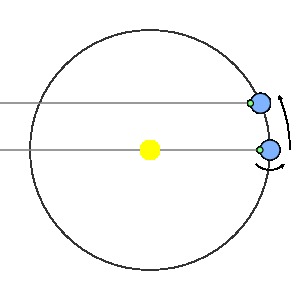
We should also consider the time required for a distant star to appear at the same point in the sky from one day to the next. Imagine that one day a star is directly behind the sun. The next day, that star will appear slightly to the west of the sun due to the motion of the earth along its orbit. A sidereal day is the time required for a star to appear in the same location in the sky, and it will be shorter than a solar day.

 

A tropical year is, informally, the length of time required for the earth to return to the same point in its orbit. Due to the earth's rotation, the number of sidereal days in a tropical year will be one more than the number of solar days. Since the length of a tropical year is 365.2422 solar days, it is 366.2422 sidereal days; therefore, the length of a sidereal day is 365.2422/366.2422 = 99.73% the length of a solar day, which is a difference of a little less than four minutes.

If our aim is to construct a sundial, sidereal time need not concern us. However, there is a useful contrast to be made. The length of the sidereal day depends only on the rotation of the earth on its axis; it is therefore nearly constant. A solar day, which depends on the speed of the earth's rotation as well as its orbital velocity, is not.

Two factors cause the length of a solar day to vary. First, the earth's orbit is elliptical rather than circular, and this causes the earth's orbital speed to vary. Second, the earth's axis of rotation is not perpendicular to the plane of its orbit, a fact well known for it is responsible for creating the seasons. When viewed from earth, the sun therefore does not move precisely in a circular path through the sky, which causes some small variation in the length of a solar day.

 

To smooth out these variations, we define a mean solar day as the length of a solar day on an imaginary earth moving at constant speed in a circular orbit with its rotational axis perpendicular to the orbital plane. The length of this day, roughly the average length of an actual solar day, is constant throughout the year, and the time that we read on our clocks is consequently defined by the mean solar day.

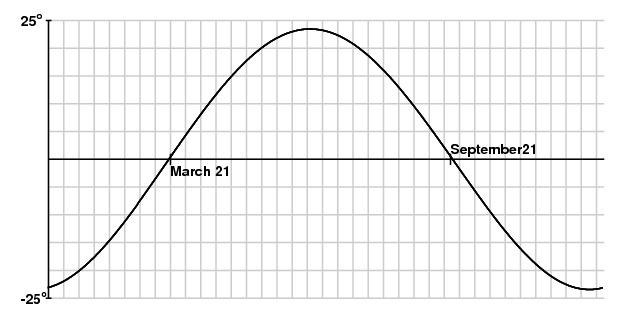
It is therefore important to consider the difference between mean time $T_m$, the time read on our clocks, and solar time $T_s$, the time read on a sundial. We call this difference the equation of time: $$ E = T_m - T_s \qquad \mbox{or} \qquad T_m = T_s - E.$$

A graph of the equation of time, which may be determined either through calculation or observation, looks like this:

 

If the equation of time is positive on a particular day, then mean time lags behind solar time. On this day, the sun will appear in the sky to the west of its location at the same time on a day on which the equation is time is zero.

For the most part, our discussion will assume the days have a constant length and then provide a correction using the equation of time toward the end.

Coordinate Systems

To keep track of the position of the sun as well as our position on the earth, we will introduce some coordinates.

Of course, it is well known that a position on the earth's surface is often described by its latitude, the angular distance from the equator, and its longitude, which is an angular measure of the distance from the position to the line of longitude through Greenwich.

 

Latitude Longitude

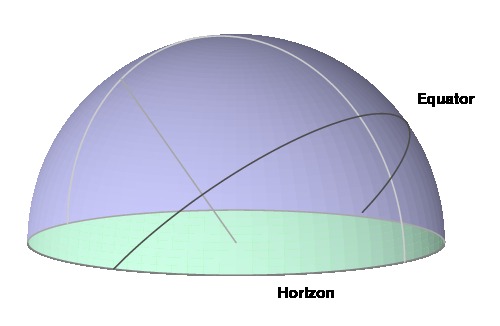
To describe the sun's position, we imagine the earth's equator projected onto the celestial sphere, an arbitrarily large sphere centered at the earth. Similar to the latitude of a position on the earth's surface, the sun's declination is the angular distance from its position to the celestial equator. Since the earth's rotational axis is not perpendicular to the plane of its orbit, the sun's declination varies over a year.

 

Meridians are lines on the celestial sphere given by projecting lines of longitude onto that sphere. Solar time is determined by the meridian on which the sun appears. Of particular importance is the meridian corresponding to the line of longitude passing through our location. We call this the noon meridian for the sun should appear on this line at noon every day.

 

On a given day, the sun appears to move in an approximately circular path about the earth; one such path, on a day in early fall or late winter, is shown below. The sun will move $360^\circ/24 = 15^\circ$ in an hour along this circular path. This means it takes four minutes to move one degree.

 

It would be quite confusing if each of us defined noon to be the time at which the sun passed through the noon meridian; for instance, if you lived one degree east of me, your noon would occur four minutes before mine. Instead, time zones are established to provide a consistent time across a large geographic region. I live in the Eastern time zone of the United States, which is five hours behind universal time; noon in this time zone is defined as the time at which the sun passes the noon meridian at longitude $5 \cdot 15^\circ = 75^\circ$ W. Time organized in this way is called legal time.

Since I live at longitude $85.96^\circ$ W, noon Eastern time will occur $(85.96-75)\cdot 4 = 43.84$ minutes before passing through my noon meridian. Any sundial constructed for this location will need to account for this difference.

Finally, many locations observe daylight savings time so an hour may need to be added to the time read on the dial.

Orienting the style

Now let's get to work constructing a sundial. Though there are many forms of dials, we will consider one of the most common dials: the horizontal dial, which consists of a planar table parallel to the ground with a style whose shadow will record the time on the table.

 

The first issue for us to consider is how to orient the style.

 

The current time is given by observing which meridian the sun is passing through. Shown here is the sun at the same time on two different days; the sun is on the same meridian, but its declination changes.

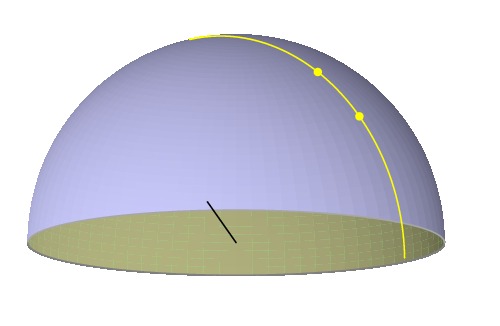Since we would like our dial to record the time accurately on every day of the year, the shadow cast by the style should lie on the same line when it is on this meridian.

Notice that a plane is formed by the sun's positions on this meridian and the center of the style. Since we would like for the style's shadow to fall in this plane, we require that the style also lies in this plane.

This property should hold at every time of day and hence for every meridian. Therefore, the style should be in the intersection of all such planes implying that the style should be oriented so that it is parallel to the earth's axis. In this orientation, the angle between the style and the table should equal the latitude of the dial's location.

Marking hour lines on the table

 

Now that we know how the style is oriented, we would like to understand how the lines should be marked on the table to indicate the hours of the day. We will use one particular line as a reference: the shadow cast by the sun when it is on the noon meridian. The convenience of this meridian comes from the fact that it intersects the horizon perpendicularly.

At another time of day, the sun will be located on another meridian, and we would like to determine the angle between the shadow cast by the style at this time and that cast at noon.

To determine the relationship between the time and the angular distance between the hour lines, construct this figure by extending tangent lines to the celestial sphere at the end of the polar axis. These lines will intersect the plane of the horizon to form a pyramid.

We are interested in the following angles. The blue angle $s$ describes the angle between the two hour lines; it is this angle that we seek. Since the style is oriented along the polar axis, the red angle is the latitude $\phi$. The green angle $h$ measures the angular difference between the current meridian and noon meridian, which depends on the current time.

We will let $C$ be the center of the dial, $S$ the end of the style, $M$ the point where the tangent to the noon meridian intersects the horizon, and $H$ the point where the tangent to the current meridian intersects the horizon.

Since the noon meridian intersects the horizon perpendicularly, we know that $\angle CMH$ and $\angle SMH$ are right angles. Also, $SM$ is tangent to the celestial sphere and $SC$ is a radius of that sphere so $\angle CSM$ is also right.

We may now apply simple trigonometry: $$ \begin{array}{rcl} \cot s & = & CM/HM \\ \sin \phi & = & SM/CM \\ \tan h & = & HM/SM. \end{array} $$

If we multiply these three expressions together, we obtain $$ \begin{array}{rc} & \cot s \sin\phi \tan h = 1 \\ \mbox{or} & \qquad \tan s = \sin\phi\tan h. \end{array} $$

Let's see this expression in action. I am writing this column at a latitude of $\phi = 42.98^\circ$ N. Where will the shadow fall on a horizontal dial two hours before my solar noon? This time corresponds to $h=30^\circ$ so we have $$ s = \arctan(\sin\phi\tan h) = \arctan(\sin(42.98^\circ)\cdot\tan(30^\circ)) = 21.5^\circ. $$

Therefore, we now know where to draw the hour line on which the style's shadow will fall two hours before (or after) solar noon.

Here is how a horizontal dial located at latitude $\phi = 42.98^\circ N$ would appear, assuming that the sun is on the noon meridian precisely at legal noon.

 

For most locations, of course, the sun is not on the noon meridian precisely at legal noon. For instance, my longitude is $85.96^\circ$ W, and my clock is set to Eastern time. Therefore, at my location, the sun lags behind the clock by $85.96 - 75 = 10.96$ degrees. This correction may be incorporated into the formula above resulting in the following dial at my location.

 

Tracing the sun's path

Now that we may use the sun's position to determine the time of day, let's go a little further and use the sun's position to determine the day of the year as well.

Here we assume that, on a given day, the sun appears to move in a circle around the earth's rotational axis; that is, we ignore the effect of the earth's motion along its orbit in one day. In this figure, two of the sun's daily orbits are shown. One orbit is in late winter or early fall while the other is in early spring or late summer.

 

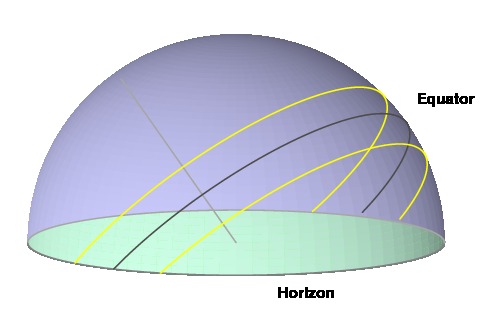
We would like to determine the path traced out by the style's shadow as the sun moves through this orbit. Before we do this, consider all the rays from the sun that pass through the tip of the style; these will form a cone.

 

The style's shadow will lie on the intersection of the dial's table with this cone. Remember now that the intersection of a plane with a cone defines a conic section, either a circle, ellipse, parabola or hyperbola depending on the angle at which the plane intersects the cone:

 

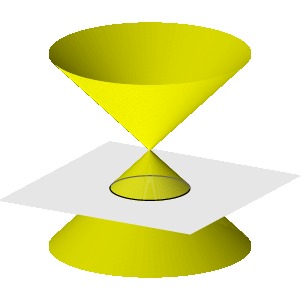Circle Ellipse
Parabola Hyperbola

A little thought shows that the sun's shadow on a horizontal dial at one of the poles will trace out a circle on a summer's day, while an elliptical shadow will be seen at slightly lower latitudes. If we live in the temperate zone, we will see hyperbolic shadows. Here is the shadow cast on a horizontal dial on a typical day in the temperate zone.

 

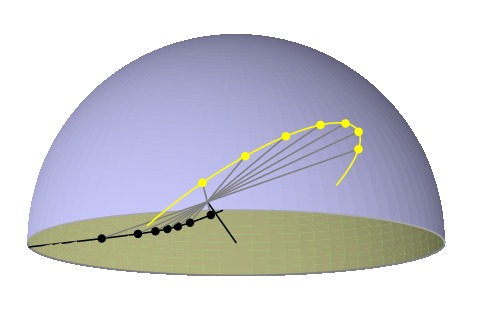
Knowing how the sun's declination varies over the year, we may trace out the sun's path on several days of the year.

 

The analemma

Up to this point, we have set up our dial using the mean sun; that is, we have assumed that the sun is moving at a constant angular velocity around the earth, which we know is not true. The error in this assumption is seen if we photograph the sun at noon, as measured by mean time, every day for a year. If mean time and solar time agreed, we would see the sun on the noon meridian every day with a varying declination. However, solar time alternately leads and lags mean time, which creates a figure eight curve called the analemma.

 

The analemma reflects the equation of time, which measures the difference between mean and solar time and which we saw earlier.

 

For instance, on a day on which the equation of time is positive, mean time lags behind solar time. Therefore, at mean time's noon, the sun will be west of the noon meridian. We can use this to correct our dial by tracing out the analemma's shadow on each of the hour lines.

 

Therefore, to read mean time from this sundial, we compare the style's shadow to the images of the analemma rather than the hour lines.

Summary

Sundials exist in an almost infinite variety of forms, reflecting their use and the creative instincts of their designers. I have aimed here to explain the design of a dial constructed by Father Ildéphonse at the convent of Cimiez-sur-Nice, which is reproduced in Rohr's book cited in the References section. This design is also reflected in the logo of the North American Sundial Society. Using principles explained in this article, it should be possible to explain most sundials that you are likely to encounter.

References

  • René R.J. Rohr, Sundials: History, Theory, and Practice, Dover, New York, 1966.

    As its title says, this delightful book covers all aspects of sundials. Of particular note is the large collection of photographs of interesting sundials.

  • Lancelot Hogben , Mathematics for the Million, W.W. Norton & Company, New York, 1993.

    Hogben uses spherical trigonometry to explain how to place the hour lines on a horizontal dial. The illustrations are particularly nice.

There are a large number of sundial related links on the Internet, including these:

Here are some general references about time and time keeping:

David AustinDavid Austin
Grand Valley State University
Email David Austin