Time and the Hour Running Through Rough Days
Posted August 2007.
There is a relatively simple algorithm to calculate the lapsed time between any two dates expressed in terms of the standard European calendar and GMT...
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
I was born in the state of New Jersey on November 27, 1941 at 2:00 AM.
Right now, as I write this, I am in Vancouver, British Columbia and the time is 2:00 PM, July 17, 2007.
What is my exact age?
Nasty question. The most straightforward way to answer it is very simple if somewhat tedious - make up a table of the different time periods involved, reduced to a single unit of time in a single time zone. For the unit of time I'll choose the day, and for the time zone I'll choose Greenwich Mean Time, for many years a kind of universal time on earth. GMT is 5 hours ahead of Eastern Standard Time and 7 ahead of Pacific Daylight Time, so I was born at 7 AM (GMT) and it is now 9 PM (GMT). We now add together
- the number of days remaining in 1941,
- the number of days elapsed from 0:00 January 1, 1942 to 24:00 December 31, 2007,
- the number of days so far elapsed in 2007.
The table runs
| |
|
|
| 17/24 |
days |
(rest of November 27) |
| 3 |
|
(rest of November) |
| 31 |
|
(rest of 1941) |
| 365 |
|
(1942) |
| 365 |
|
(1943) |
| 366 |
|
(1944) |
| ... |
|
... |
| 366 |
|
(2000) |
| ... |
|
... |
| 365 |
|
(2006) |
| 181 |
|
(January - June, 2007) |
| 16 |
|
(July 1 - July 16) |
| 21/24 |
|
(elapsed so far July 17) |
|
making a total of 23973 days and 14 hours. The only tricky thing is how to deal with the year 2000, as I'll explain in a moment.
This is not only somewhat tedious, it is just complicated enough to be prone to error. For short periods it can be done on a spreadsheet, laid out more or less as the table indicates. There is one mildly interesting mathematical question that arises - is there a good spreadsheet formula for calculating the length of a year? In the Gregorian calendar, the number of days in most years is 365, but very fourth year is a leap year with 366 - except that years which are multiples of 100 are not leap years - except that years which are divisible by 400 are leap years. So 2000 is a leap year---the only exceptional thing about the year 2000 is that it is not exceptional!
Another mildly annoying feature of the Gregorian calendar is that the number of days in a month varies rather erratically, so calculating the time elapsed between one day of the year and another is a bit painful.
These observations make it all the more remarkable that there is a relatively simple algorithm to calculate the lapsed time between any two dates expressed in terms of the standard European calendar and GMT.
Suppose a date is given in year, month, day format, expressed numerically. Let these be Y, M, D in numbers, where M ranges from 1 to 12) and D is the number of days elapsed since midnight at the beginning of the month. Thus noon on January 1 has D=0.5. The basic idea of the algorithm is to convert the date into a form more convenient for computation. The conversion turns a date expressed in the Gregorian calendar into a single number - its Julian day number, which is the number of days elapsed since a certain fixed date. To find the length of time (in days) that has passed between two distinct dates, calculate the corresponding Julian day numbers and take the difference.
The algorithm
How does one calculate the Julian Day Number? I give here a slight modification of the method presented in Wikipedia, which I shall then explain. It works only for dates subsequent to 4800 B. C., but this is hardly a serious restriction since after all no dates were recorded anywhere on the planet before then.
In Western culture since the early middle ages, there have been two calendars widely used, the Julian and the Gregorian. The Julian calendar was in important aspects the one put into place by Julius Caesar. It assumed a year of length 365.25 days, which was a bit longer than the true one of approximately 365.2422 days. It was used more or less continuously for more than a millennium, but as time went on it was realized that the date on which certain events happened, such as the equinoxes, were not what they had been in Roman times. For this reason it was replaced by the Gregorian calendar, which was much more accurate. In much of Europe the new one was put into place at midnight on October 4, 1582, so that the following day was October 15! It took a long time before the rest of Europe accepted the new scheme. It wasn't until 1752 that England adopted the Gregorian calendar, which it called New Style as opposed to Old Style. September 2, 1752 (O.S.) was followed by September 14 (N.S.).
Because the Middle Ages recorded dates in the Julian calendar, it is conventional to use the Julian calendar through October 4, 1582 and the Gregorian one after that, although in accounts of English history through the 18th century dates are often recorded in both forms, the Julian calendar in which English contemporaries recorded them as well as the Gregorian calendar in which the French (among others on the Continent) did so.
Therefore, the algorithm has to deal with two separate cases, depending on whether the date is given according to the Julian or the Gregorian calendar.
Suppose the date is given as Y, M, D (in either calendar). The year for dates B. C. are expressed as negative numbers, where 1 B.C. is given as 0, 2 B.C. as -1 etc. Set
a = [ (14-M) / 12 ]
y = Y + 4800 - a
m = M + 12a - 3
Here [x] is the floor function, the integer just below x. Thus [3] is 3, and so is [3.1].
For a Gregorian date the Julian day is then
(D - 0.5)+ [153m+2/5] + 365y + [y/4] - [y/100] + [y/400] - 32044
while for a Julian date it is
(D - 0.5) + [153m+2/5] + 365 y + [y/4] - 32082.
To see how it works, for my birthday we get
a = [ (14-11) / 12 ] = 0
y = 1941 + 4800 - 0 = 5741
m = 11 - 3 = 8
365y + [y/4] - [y/100] + [y/400] = 2462099
[153*m+2/5] = 245
JDN = 25.7917 + 245 + 2462099 - 32044 = 2430325.7917
and similarly for today JDN = 2454299.375, making as before a difference of 239373.5833 days. One very good feature of the formulas is that they are not hard to put into a spreadsheet.
What the terms mean
Let's look at each of the steps in the calculation.
(1) Set
a = [ (14-M) / 12 ]
y = Y + 4800 - a
m = M + 12a - 3
If M=1 or 2 (the month is January or February) this sets a=1, y = (Y-1)+4800, M=M+9, otherwise (M > 2) it sets a=0, y=Y+4800, m=M-3. Adding 4800 is a somewhat arbitrary shift that guarantees that y > 0 for historical dates.
This part of the formula has historical roots. In effect, January and February become the last months (10 and 11) of the previous year, so we are introducing a new calendar, one in which the first day of the year is March 1 instead of January 1. This is a good idea mathematically, since in this new calendar February, the only month with a variable number of days, is last. Hence the number of days from the start of the year to a given date does not depend on the year, as it does in our own calendar.
This is such a great idea that you might wonder why it hasn't been done before! Now our calendar is derived from the Roman one, later amended in a first version by Julius Caesar and then in a second by Augustus. In the original Roman calendar, the beginning of the year was indeed March 1. There are still traces of this in our current calendar, because the names of the months September, October, November, and December are cognate with the Latin numbers 7, 8, 9, 10. It was Julius Caesar who made January the first month. On the other hand, though, it was also he who decreed that the variable day occurs in February. One never knows, do one?
(2) If the date is October 4, 1582 or earlier (when the Julian calendar was in effect), set S = 365y + [y/4], otherwise (we are using Gregorian dates) set S = 365y + [y/4] - [y/100] + [y/400].
The ancient Roman calendar was chaotic. Julius Caesar, acting according to Pliny the Elder with the advice of the Alexandrian mathematician Sosigenes, reformed it in about 46 B.C. The main effect was to bring the length of the calendar year into better synchronization with the true length of a solar year. Since the number of days in a solar year is not an integer, in order to maintain this synchronization the length of a calendar year must vary from time to time. In the Julian calendar, three out of every four years had 365 days and the fourth year 366. The Julian calendar, in effect, assumes the true length of a solar year (say from vernal equinox to vernal equinox) to be 365.25 days. This is not correct, and overshoots the mark a bit, since the true solar year is very close to 365.2422 days. Even in Roman times the better estimate of 365.2467 days was known to experts, and I have not seen any explanation of why the Julian scheme was accepted when it was known not to be as accurate as it might have been.
By the year 1500 or so, it was obvious to anybody who knew his history that the date of the vernal equinox, which is a natural event to use for recording annual periodicity, was about 10 days later than it had been in Roman times. After a great deal of discussion, Pope Gregory XIII, acting with the advice of several Jesuit mathematicians and astronomers, decreed that a change would be made official. In Catholic Europe, the next day after October 4, 1582 was October 15. In the rest of Europe this reform was apparently considered an attempt by the Roman Catholic Church to subvert the true order of things, and in effect to steal days away from people. There seems even to have been current a common opinion that they were days removed permanently from one's life span. The change was, however, adopted gradually by the rest of Europe over a period of several centuries---by England in the middle of the 18th century, by Russia only after the revolution of 1917.
Pope Gregory's decree arranged that the dates of the equinoxes would agree with those of ancient times, but it also modified the Julian scheme of leap years in order to maintain synchronization. Every 100th year would not be a leap year, except that every fourth century break would be. Thus 1600 and 2000 were leap years in the Gregorian scheme, while 1700, 1800, and 1900 were not. This amounts to estimating the year at 364.2425 days long. In our shifted calendar, these numbers must be moved back one year, so that year y normally has 366 days if y+1 is divisible by 4.
The number S counts the number of days elapsed from midnight of March 1 in the virtual year 0 of the relevant calendar to midnight of March 1 of year y.
(3) Add T = [153m+2/5] to S. This is, mathematically, the most interesting term. The following table shows what it does:
| m |
T |
Differences |
|
Month |
| 0 |
0 |
31 |
|
March |
| 1 |
31 |
30 |
|
April |
| 2 |
61 |
31 |
|
May |
| 3 |
92 |
30 |
|
June |
| 4 |
122 |
31 |
|
July |
| 5 |
153 |
31 |
|
August |
| 6 |
184 |
30 |
|
September |
| 7 |
214 |
31 |
|
October |
| 8 |
245 |
30 |
|
November |
| 9 |
275 |
31 |
|
December |
| 10 |
306 |
31 |
|
January |
| 11 |
337 |
- |
|
February |
|
In other words, the number T(m) counts the number of elapsed days from 0:00 on the previous March 1 of that year to 0:00 of the first day of month m. It is not at all obvious that there exists a simple arithmetical formula for T, much less how the valid formula T=[(152m + 2)/5] was arrived at. These matters are of genuine mathematical interest, and will be dealt with once two other parts of the formula are explained.
(4) Add D-0.5 to the sum so far.
The Julian day starts at noon. This number is the number of days elapsed since the beginning of the current month.
(5) Subtract either 32044 (Gregorian) or 32082 (Julian).
These numbers differ by 1 from the Wikipedia article since I take D=0.5 to be noon on the first day of the month, whereas Wikipedia would take D=1.5 at that moment.
The point of these subtractions is to set the origin of the calendars. The date now settled on as the origin of the Julian Day numeration was chosen for historical and religious reasons by Joseph Scaliger in the 16th century to be January 1, 4713 B. C. This somewhat arbitrary choice was made by the Scaliger on the basis of some arithmetic combining three cycles each of several years in length---the Julian cycle, in which days of the week repeat every 28 Julian years, the Metonic cycle, which measures an approximate cycle of the relative positions of the sun and the moon (which determine the occurrence of Easter in the Roman Catholic Church), and the indictio, a period important in Roman tax administration. For simple arithmetical reasons, the combination of these cycles forced the starting date of the new Julian reckoning to be January 1, 4713 B.C. The details can be found in the book by Otto Neugebauer listed among the references. This scheme is surely one of the first examples of "legacy code," but it is probably still used in modern astronomy because essentially all astronomical data originated after Julian date 0. (The 11th edition of the Encyclopaedia Britannica asserts that Joseph Scaliger was the most famous scholar of all time! So fickle is fame.)
Approximating sequences by formula
The number of days T elapsed from March 1 to day 1 of month m, where m varies from 0 (March) to 11 (February) is given by the formula
T = [(153m+2)/5] .
This is the solution in this particular case of a more general problem: Which empirically given functions F(n) on a range of integers, with integral values, can be given by a formula of the type F(n) = [an + b] where a and b are real numbers?
In this particular case, the function we are calculating is given by the table we have seen above. I repeat the part of the table we need:
| |
|
|
|
|
|
|
|
|
|
|
|
|
| m: |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
| T: |
0 |
31 |
61 |
92 |
122 |
153 |
184 |
214 |
245 |
275 |
306 |
337 |
| T-30m: |
0 |
1 |
1 |
2 |
2 |
3 |
4 |
4 |
5 |
5 |
6 |
7 |
|
As the third row of this table shows, we can write T(m) = 30m + U(m) where U(m) is a function that we can manipulate more easily. The original approximation for T(m) becomes the approximation [(3m+2)/5] for U(m). Here is a graph showing how this works---the red bars show U(m), the black slope line the graph of [(3m+2)/5].
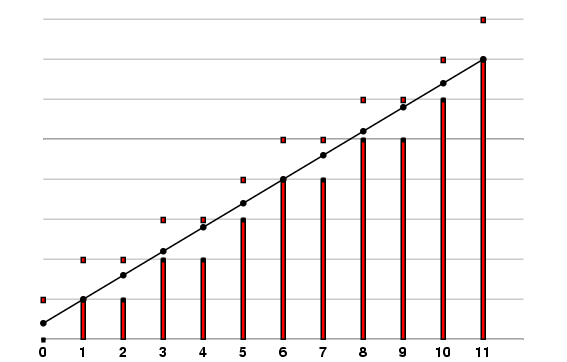
What the graph shows is that f(m) = [(3m+2)/5] is a formula for U(m) because for m=0, 1, ... 11 the value of (3m+2)/5 lies between U(m) and U(m) + 1. We can see this even more clearly by picturing the graphs of f(m) and f(m)+1 as stairs:

So our graph must pass between lower and upper stairs. But a line will lie above the lower stairs precisely when it lies above the lower region pictured below, and similarly it will lie below the upper stairs when it lies below the upper region in the picture. These are known as the convex hulls of the stairs, and they are easy to construct. So our straight line exists lying between the upper and lower stairs precisely when there is a gap between the two convex hulls, as there is here. And any line passing from x=0 x=11 that passes through the gap will do the trick.
There is a simple procedure for finding convex hulls in two dimensions, but here it would be quite feasible to find a line with a ruler and pen.

Describing all possible lines
We don't have to rely on the human eye to find possible values of a and b. As the following picture shows, the line y=ax+b has to pass between each of twelve vertical segments.
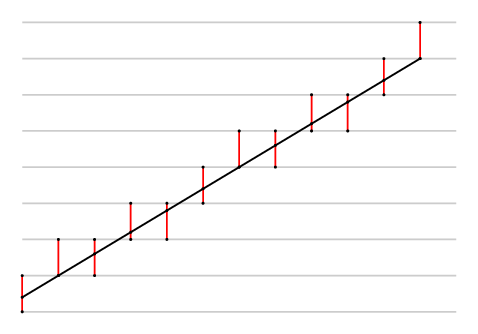
Each of the intervals gives rise to a condition on a and b, giving us 12 in all:
| |
|
| |
0 ≤ b < 1 |
| |
1 ≤ a+b < 2 |
| |
1 ≤ 2a+b < 2 |
| |
2 ≤ 3a+b < 3 |
| |
2 ≤ 4a+b < 3 |
| |
3 ≤ 5a+b < 4 |
| |
4 ≤ 6a+b < 5 |
| |
4 ≤ 7a+b < 5 |
| |
5 ≤ 8a+b < 6 |
| |
5 ≤ 9a+b < 6 |
| |
6 ≤ 10a+b < 7 |
| |
7 ≤ 11a+b < 8 |
|
Each of these describes a region in the two dimensional plane in which a and b are coordinates. Below are the regions associated to the conditions 0 ≤ b < 1 and 1 ≤ a+b < 2.
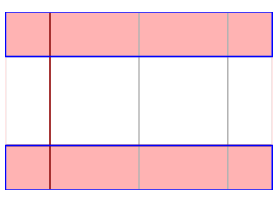
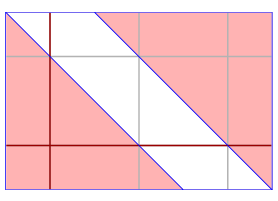
The figure on the left shows where both these conditions are satisfied, and the one on the right shows where in addition 1 ≤ 2a+b < 2 ...

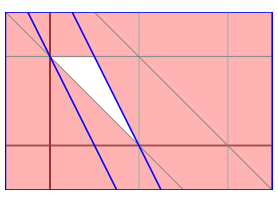
... and here we add the conditions 2 ≤ 3a+b < 3, 2 ≤ 4a + b < 3:


What we see is that the final region of all allowable (a,b) is going to be the inside of a convex polygon. Zooming in a couple of times on the figure taking into account all of the inequalities, we see:
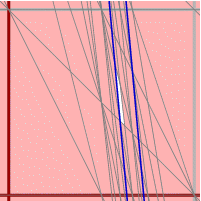
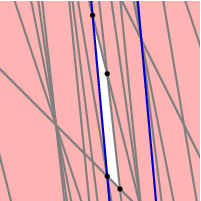
In other words, the region of allowable (a,b) is a quadrilateral. One can calculate without too much trouble that its vertices are the lines through the points (1,1) and (11,7); (1,1) and (9,6); (4,3) and (11,7); (4,3) and (9,6). (This is an interesting exercise that can be done in many ways.) Explicitly, the vertices of this region are (3/5,2/5), (3/5,3/5), (5/8,3/8), and (4/7,5/7). It is the first that is used by the algorithm in Wikipedia, but to tell the truth it's a bit dangerous to do so. Computers work in arithmetic of base two, and 1/5 cannot be represented exactly. The diagram on the right above suggests that (0.601,0.401) would be safer.
Convexity
Let me summarize. We are given an integer sequence {am} where 0 ≤ m ≤ n, and want to know whether there exist a and b such that am = [am+b], and if so find a suitable pair. The condition on a and b is that am ≤ am+b < am+1 for 0 ≤ m ≤ n. The region of possible (a,b) is the intersection of a collection of 2n+2 half-planes am ≤ am+b, am+b < am+1 for m=0 to n. The mathematical problem is to find whether that region is empty, and if it not to find its extremal vertices. This is a two-dimensional example of the classic problem of linear programming---to move back and forth between the two ways of describing a convex polyhedron, (a) as the convex hull of its vertices, (b) the region bounded by its faces.
In two dimensions there is a simple solution. Adding one inequality after the other, one has to deal with this problem: Given a polygon with vertices Pi and an inequality ax+by+c ≤ 0, find the vertices of the subset of the polygon where the inequality is satisfied.
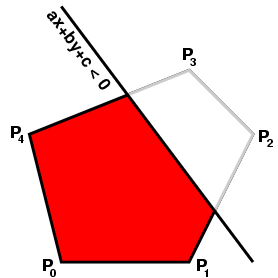
The solution is to traverse the vertices and record where the line is crossed.
Augustun daze
The original calendar proposed by Julius Caesar was considerably more rational than the one we now use. The month of August (which was called Sextilis in those days before Augustus became emperor, as July had been called Quintilis before Julius came along) had 30 days, September had 31, and so on in alternation. The formula for calculating the number of days elapsed from March 1 was then very simple. But the month of July was dedicated to Julius Caesar, and when in turn the month of August came by decree to be dedicated to his successor Augustus, it was insisted that August be as long as July. A day was stolen from February, and then the alternation of sizes was changed to make September shorter than August, and alternating 31/30 from that month on. It's not very amazing that these changes took place, but rather more amazing that we still live with the minor annoyances the vanity of a Roman emperor created.
To find out more
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal , which also provides bibliographic services.

















