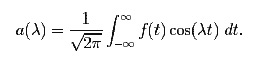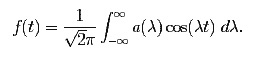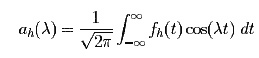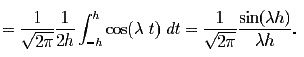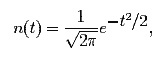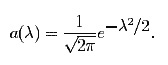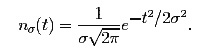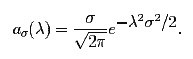The Mathematical Uncertainty Principle
Posted November 2005.
There is a purely mathematical phenomenon that closely parallels the Heisenberg Uncertainty Principle...
Tony Phillips
Stony Brook University
tony at math.sunysb.edu
Introduction: The Speeding Physicist
A physicist is stopped for speeding. "No, Officer, I don't know how fast I was going. But I do know exactly where I am." The joke is built on the implicit reference to Heisenberg's Uncertainty Principle, a bedrock of modern physics: The position and the momentum of an object cannot both be measured exactly, at the same time. Quantitatively, Δ x Δ p ≥ $\frac{h}{4\pi}$, where Δ x is the uncertainty in the measurement of position x, Δ p the uncertainty in the measurement of momentum p, and h is Planck's constant. In MKS units, $\frac{h}{4\pi}$ works out to be approximately 0.5 10-34kg m2⁄s.
The Speeding Electron
For example, the mass m of the electron is close to 10-30 kg. So any simultaneous measurements of its positon x and velocity v are constrained by Δ x Δ v ≥ 0.5 10-4 m2⁄s, using p = mv. If in some experiment we can measure the position of an electron to within one micron, or 10-6 m, then the uncertainty Δ v must be greater than 0.5 10-28/10-30 = 50 m/s: we can only know its velocity to within plus or minus 50 meters/sec. (I checked with our Physics Department and was told not to worry: An electron in an orbit of that diameter typically travels at around 30,000 m/s.)
Singing into the Piano
There is a purely mathematical phenomenon that closely parallels the Heisenberg Uncertainty Principle.
Qualitatively, it can be understood as the problem of ascribing to a burst of sound both a location t in time and a frequency λ. It is clearly hard to pinpoint the frequency of a very short burst: If Δ t is small, then the indeterminacy Δ λ will be large. Conversely, sound at one exact frequency (Δ λ = 0) would correspond to a perfect sine wave, with no beginning or end (Δ t = ∞).
To make this more precise we use the mathematical formalism of the Fourier transform. Here again the analogy with sound is helpful. If you sing a note into a piano while holding down the damper pedal, so all the strings are free to vibrate, you will hear the piano duplicate the sound of your voice. What is happening? Each of the piano strings has its own sound, which does not sound like your voice at all. But when the strings are excited by your voice, each one resonates to the extent that its frequency is present in your voice. When you stop singing the strings continue to vibrate, each with the appropriate amplitude, and your voice is perpetuated.
The Fourier transform acts like a piano with infinitely many strings, giving each frequency λ between 0 and ∞. The analogue of a sound burst (which could be the pressure-wave due to your voice) is a time-varying function f(t). The amplitude picked up by the string with natural frequency λ becomes
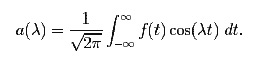
This is a finite integral for any value of λ if you only sing for a finite time, or if, more generally, the absolute value of f has a finite integral from -∞ to ∞. We'll call such {C}a function "absolutely integrable."
The mathematical analogue to the piano's prolonging your voice after you stop singing is the equation
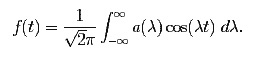
The string with fundamental frequency λ is vibrating with amplitude a(λ); the integral sums up all those vibrations to reconstitute your voice.
What about Phases?
To reconstruct an arbitrary f(t) exactly requires some more information, since advancing or retarding the phase of a(λ) cos(λt), one of the harmonic constituents, gives a different function (although it sounds the same to the ear). If that component is switched on δ seconds earlier, it is represented by a(λ) cos(λ(t + δ)). The trigonometric identity for cos(a+b) rewrites this as a(λ)[ cos(λt)cos(λδ) - sin(λt)sin(λδ)] which we can regroup as a(λ)cos(λδ) cos(λt) - a(λ)sin(λδ) sin(λt) = A(λ)cos(λt) + B(λ)sin(λt), so the exact synthesis in general will require sines as well as cosines. To avoid this slight complication, we will restrict attention to even functions f (t): those satisfying f (-t) = f (t); for these, cosines are sufficient.
The Fourier Transform for Even Functions
Theorem. If f (t) is an even, absolutely integrable function then
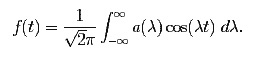
where
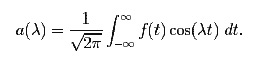
The theorem holds as stated for a continuous function f (t); if the function has a finite number of jump discontinuities t1, ..., tp (i.e. points where the left-hand limit f (ti-) is different from the right-hand limit f (ti+) , then the dλ integral at one of those points splits the difference and gives (1⁄2)[f (ti+) + f (ti-) ].
Some Simple Examples of Even Functions and Their Fourier Transforms
The most elementary functions with a finite integral on the whole line are constant on a finite interval and zero everywhere else. They will be even functions if that interval is centered about t = 0. Let us consider the family fh of functions defined by
fh(t) =
|
0 if t < -h 1/2h if -h ≤ t ≤ h 0 if h < t
|
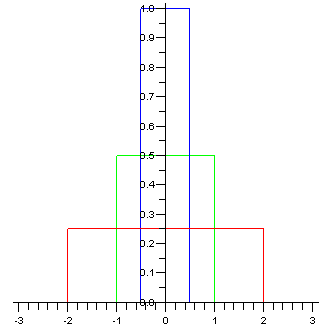
The graphs of f h for h = 0.5 (blue), 1 (green), 2 (red). The horizontal and vertical axes are scaled differently, but these graphs all enclose the same area. They are analogous to a family of sound bursts of varying lengths, but of the same total power.
The Fourier transform of fh can be calculated by anti-differentiation:
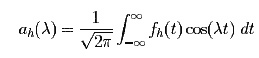
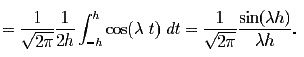
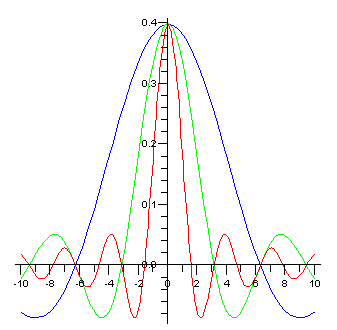
The graphs of ah for h = 0.5 (blue), 1 (green), 2 (red), colored the same as the graphs of the functions they transform. Note that the width of the transform is inversely proportional to the width of the function.
(The direct reconstruction of fh from ah, which follows from the Theorem, can also be achieved by a fairly elementary but roundabout method. See, for example, David L. Powers, Boundary Value Problems, 4th Ed., Section 1.9).
Uncertainty Principle for the Fourier Transform
The fh and their transforms ah show the uncertainty principle for the Fourier transform at work. Roughly, the more tightly localized the f (t) signal is (the shorter the duration of the sound burst), the less tightly localized the a(λ) distribution must be (the larger the spread in frequencies); conversely, the tighter you cluster the frequencies, the wider the f (t) distribution must be. This principle has very precise and natural formulation for normal probability distributions.
The Normal Distribution Function
A probability distribution function f is a non-negative function with total integral equal to 1. (The fh defined above are probability distribution functions). One very important example is the normal distribution with mean zero and standard deviation 1:
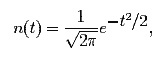
an even function. The Fourier transform of this function is essentially the same function:
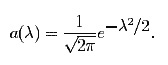
(This calculation is not too difficult, using the identity cos(λ)=(1 ⁄ 2)(eiλ + e-iλ) and completing the squares in the resulting exponents.)
The Uncertainty Principle for Normal Distribution Functions with Mean Zero
The uncertainty principle takes a sharp form when we adjust the normal distribution to have variance σ2 (equivalently, standard deviation σ), by letting
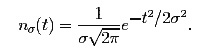
Then the same calculation as above yields
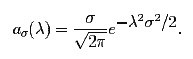
In words, the Fourier transform of a normal distribution with mean zero and variance σ2 is a normal distribution with mean zero and variance 1 ⁄ σ2. Let's use the notation Ff for the Fourier transform of f (the function we have been calling a), and write D for variance. Then the relation between the variances of a normal probability distribution function with mean zero and its Fourier transform can be expressed in "uncertainty principle" form as
D(Ff ) D(f ) = 1.
And More Generally ...
{C}This property does not generalize to arbitrary probability distribution functions (p.d.f.'s) because Ff may not be a p.d.f. at all (it was not for our fh examples) and its variance may not be defined. On the other hand, the Fourier transform preserves the integral of the square of a function (this is the Plancherel Theorem). So if f 2 is a p.d.f., then (Ff )2, which is automatically non-negative, will also have total integral equal to 1: it is also a p.d.f. Now our uncertainty relation does generalize, and becomes:
D((Ff )2) D(f 2) ≥ 1/2.
The resemblance between this statement and Heisenberg's uncertainty principle is not coincidental, but is due to the relation between position and momentum in quantum mechanics. They are conjugate variables, and the corresponding probability amplitudes are therefore related just as f 2 and (Ff )2, except with the scale change that produces the extra $\frac{h}{2\pi}$.
Tony Phillips
Stony Brook University
tony at math.sunysb.edu
NOTE: Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal, which also provides bibliographic services.