3. Voting and Elections: Election Decision Methods Voting and Elections: Election Decision Methods
Feature Column Archive
3. Election Decision Methods
Consider the election below:
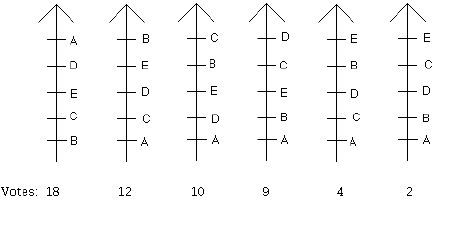
Here are five different procedures for selecting a winner for the election shown.
1. Plurality
Count how many first place votes each candidate receives. The winner is the candidate with the largest number of first place votes.
2. Run-off election
Count how many first place votes each candidate receives. If no candidate receives a majority, declare all candidates except those two who have gotten the largest number of first place votes as losers. Now, conduct a new election based on the preferences of the voters for these top two vote getters at this stage.
Note that since we have preference ballots, this procedure does not require voters to go to the polls again. It is true that voter preferences might be changing with time (which happens due to actions that candidates are regularly taking that change the views of the electorate), so if voters provide preference ballots at a later time they may be different from those collected originally. In our discussion here, the run-off method is based on the use of the original preference schedules with out asking for a new set of preferences as a result of the first stage of the process. This method is sometimes called an instant run-off.
3. Sequential run-off election
If no candidate gets a majority based on first place votes, eliminate the candidate with the fewest first place votes and hold a new election based on voting only for the smaller collection of candidates. Repeat the process until some candidate receives a majority of the first place votes.
This procedure is related to a method of selecting a group of candidates for office using preference ballots which is known as the single transferable vote, or Hare's method. This method has been used in Australia and Ireland.
4. Borda count
Given a preferential ballot and a candidate on the ballot, assign candidate X a number of points equal to the number of candidates below candidate X on the preference ballot. The Borda count procedure assigns as the winner of an election the candidate with the highest Borda count.
For example, the Borda count applied to the ballot below would yield 2 points for Gore, 1 point for Nader and 0 points for Bush.
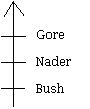
5. Condorcet
Consider all possible two-way races between candidates. The Condorcet winner, if there is one, is the one candidate who can beat each other candidate in a two-way race with that candidate.
If you carry out these 5 election methods on the 55 voter election above, something remarkable happens. There are 5 different winners! Each of the candidates will be the winner depending on what election decision method is used.
The way that voting and elections are often described in democratic societies is that the results are somehow the inevitable consequences of the input of the voters. The winner of the election is in some sense the people's choice, growing in an organic way out of the desires the electorate has for which person should lead it. However, the result of the election above calls this into question. The results of this election depend on the choice of system used to carry out the election: the ballots are the same in each case, only the result in each case is different. Each of these election methods can be accompanied by an appealing explanation to support it. Furthermore, human ingenuity offers other methods as well. Here are two additional methods. For each ballot, give a candidate one point if the voter ranks this candidate at the median level or above. This might be considered a form of approval voting where it is reasoned that a voter approves any candidate who the voter ranks above the middle. However, remember here we are assuming one must rank all candidates. Thus, one might not really be able to conclude that voters approve of any but a top choice. Another fascinating method was developed by the American psychologist Clyde Coombs (1912-1988). Coombs' method is based on avoiding electing candidates who are ranked low on preferential ballots. The method works as follows: If no candidate gets a majority based on first place votes, then eliminate the candidate who at this stage has the largest number of last place votes. A new election is made with this candidate deleted from the original preference ballots and the procedure described is repeated until a single candidate gets a majority. You can verify that for the election above, E is the Coombs winner.
Many people, when they see the Condorcet method for the first time, find it very appealing. If a candidate can beat every other candidate in a two way contest, why should that person not be the winner of the election? Whether or not you find this point of view convincing, there is a difficulty with the Condorcet method, as was first demonstrated by Condorcet himself.
Consider the set of ballots below, and compute the results of the two-way races:
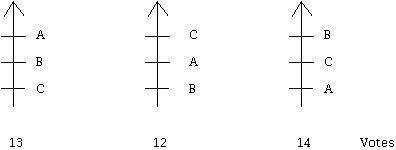
A beats B by 25 to 14, B beats C by 27 to 12, while, surprisingly, C beats A by 26 to 13. Thus, there is no candidate who can beat all the other candidates in a two-way race. This example which was constructed by taking the ordering of the candidates in the first preference schedule and moving the bottom candidate to the top, keeping the other candidates in the same order to get the second preference schedule, and so on, can be generalized to achieve a similar example with any number of candidates.
This situation shows that Condorcet's method can not serve as described as an election decision method because for some elections it will decide no winner, which is not acceptable. Many methods have been devised to complete the Condorcet method by choosing a winner in some manner when there is no Condorcet winner. Two such methods are one due to Duncan Black which, if there is no Condorcet winner, uses the Borda count to decide a winner. Another proposal is due to Edward John Nanson. (Nanson lived from 1850 to 1936. Born in England, he taught mathematics for many years at the University of Melbourne.) Nanson's method is an elimination method based on the Borda count. The Borda count is computed for each candidate and the person with the lowest Borda count is eliminated and a new election held using the Borda count until a single winner emerges. An interesting theorem is that if there is a Condorcet winner, this method chooses that person. If there is no Condorcet winner then some candidate, not necessarily the same as the Borda count winner, is chosen.
The paradoxical fact, until one's intuition has been trained, that deciding elections by two-way races does not guarantee that if A beats B in a two way race, and B beats C in a two-way race, that A will be able to beat C in atwo-way race is but one of many paradoxical results in the theory of elections. Many of these paradoxes take the form that otherwise appealing election methods do not obey some intuitively attractive fairness rule (axiom). Though a system of run off elections is appealing to many people, there are numerous examples to show that there are elections where, if voters modify their preference schedules to raise an otherwise winning candidate's position on some ballots the result is the defeat of this candidate. Examples of this kind pepper the literature of elections and social choice theory, and Kenneth Arrow's work helps put some perspective on them.
- Introduction
- Ballots
- Election Decision Methods
- Enter Kenneth Arrow
- Evaluating Election Systems
- References
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance





