Remembering Bill Thurston (1946-2012)
Thurston not only achieved important results in mathematics but attempted to share his expertise, insights and enthusiasm for mathematics with those he came in contact with. ...
 Joseph Malkevitch
Joseph Malkevitch
York College (CUNY)
Email Joseph Malkevitch
Introduction
There are superstars in all disciplines--Darwin in biology, Pauling in chemistry, Newton in physics, Mozart in classical music, and Freud in psychology. Mathematics, too, has superstars, and Newton qualifies in this category, too. Those concerned with mathematics education debate whether one is born with mathematical talent or, if given a certain ability threshold, someone can be nurtured into greatness in mathematics. And many people gain tremendous satisfaction in the study of and careers in mathematics without being superstars and or even stars. In some fields talent shows up in some people very young, Mozart being a good example, and it is often stated, not fully accurately, that mathematicians do their best work quite earlier in their careers. However, when it comes to recognizing mathematical talent, perhaps mathematics' most prestigious award, the Fields Medal, comes with the requirement that it must be awarded to someone prior to the age of 40! (point of emphasis, not factorial) And yes, by 40 Mozart and Schubert were dead, as were the mathematicians Niels Henrik Abel (1802-1829) and Évariste Galois (1811-1832). In more recent times these mathematicians of great promise died at an early age:
- Srinivasa Ramanujan (1887-1920),
- Mikhail Yakovlevich Suslin (1894-1919),
- Andreas Floer (1956-1991), and
- Oded Schramm (1961-2008).
Mathematicians come in a tremendous variety of flavors: those who have done impressive work in many parts of mathematics and those who do spectacular work in a narrow part of mathematics; those who contribute to mathematics only and those who contribute to other areas of knowledge as well; those who talk only about mathematics and those who seem equally at home discussing politics, music, art, and literature as well as mathematics. Where does musical and mathematical talent come from? Certainly mathematical talent can run in families. Many members of the Bach family became musicians and several members of the Bernoulli family became mathematicians. George David Birkhoff's son Garrett was a mathematician. While Mozart's father was a competent musician, who could have predicted that his son would become who he did? The mathematics community and the mathematics education community still debates nature versus nurture in mathematical talent and how one can look for those women and men who could contribute to and find happiness in careers in mathematics.
Mathematics and Statistics Awareness Month is designed to call the attention of the public to the wide array of charms that mathematics can offer anyone. This article is a tribute to the distinguished American mathematician William Paul Thurston. Thurston won a Fields medal, an honor he shared with Alain Connes and Shing-Tung Yau in 1982. Thurston not only achieved important results in mathematics but attempted to share his expertise, insights and enthusiasm for mathematics with those he came in contact with.

Photo of William Thurston
A brief biography of William Thurston
Bill Thurston's parents were not mathematicians but his father had a background in physics and engineering. His mother was interested in sewing, which perhaps explains why Thurston took an interest in clothing and fashion, or it may be explained by his concentration on understanding the way surfaces behave. Maybe the complex behavior of cloth may have helped his thinking along. Many distinguished mathematicians have had their training at "name brand colleges," but Thurston went instead to a "start up" college in Florida: New College.
New College was born as a private college, with its first class starting there in 1964 but it now operates as the New College of Florida and is a public university. Thurston graduated in 1967 and went to the University of California, Berkeley to pursue a doctorate degree. He completed his degree there with a thesis entitled "Foliations of Three-Manifolds which are Circle Bundles" in 1972. Thurston's academic lineage is of interest because his advisor Morris Hirsh was in turn the student of two people with roots in topology: Edwin Spanier (who studied with the topologist Norman Steenrod) and Stephen Smale, himself a Fields Medal winner who studied with Raoul Bott.
Thurston began his academic career by spending a year at the Institute for Advanced Study at Princeton. Later he taught at MIT as an assistant professor and at Princeton University as a professor. In 1991 Thurston left Princeton to return to the University of California, Berkeley. Two years later he became the director of the Mathematical Sciences Research Institute (founded in 1982) in Berkeley, often referred to as MSRI. MSRI promotes mathematics in many ways, including having regular research seminars and longer term events going on for about a semester where scholars on a particular theme are invited to visit and interact on this theme. Such programs might be on harmonic analysis, analytic number theory, or geometric and topological combinatorics. The selected theme topics rotate through a wide range of areas of mathematics and its applications. During the period he directed MRSI Thurston attempted to broaden its activities and to include a component of promoting public awareness of mathematics.
Thurston left MRSI in 1997 to move to the University of California, Davis and in 2003 left Davis to become a professor of mathematics at Cornell University. In 2011 he was diagnosed with a melanoma and he died in 2012. A conference was held in his memory at Cornell in 2014.
In addition to the Fields Medal, Thurston won many additional honors. These included the Oswald Veblen Prize in Geometry (1976) and the Leroy Steele Prize (2012). In 2005 the first AMS Book Prize was awarded to Thurston for the book Three-dimensional Geometry and Topology. Lecture notes on which this book was based had been circulating for many years and influenced many people before they were codified into this book. As noted, the Fields Medal is only awarded to individuals who are younger than 40 at the time the prize is awarded. Certainly it is common for Fields Medal winners to continue to do impressive mathematics after they are awarded the prize, which was certainly true of Thurston. There are also mathematicians who do not get Fields Medals and for whom some of their best work is done after they are 40. In recent years there have been newer highly prestigious prizes which are not tied to age. These include the Shaw Prize, the Abel Prize, and the Wolf Prize.
Comments?
Thurston and manifolds
Mathematics has many areas such as algebra and geometry but it is often hard to classify where a particular piece of mathematics "belongs." Thus, people speak of geometric algebra and algebraic geometry. While most people would describe Thurston as a topologist, he also did work in geometry and some of what he did was described as geometric topology.
Geometers and topologists are interested in surfaces. You are familiar with many kinds of surfaces, planes, spheres, cones, and donuts (torus, plural tori). A manifold is a special kind of surface with the property that at every point on the surface, the surface looks like Euclidean space. More precisely, a manifold has the property that every point of the manifold (surface) is the center of a set topologically equivalent to a (open) Euclidean ball. A Euclidean ball is the set of points whose distance from a fixed point is less than or equal to a fixed real number r (the radius of the ball). Balls come in two flavors, open balls which consist only of those points which are strictly less than r, while closed balls also include the points which are exactly r units from the center. The interior of a circle is an open 2-dimensional ball and is often referred to as a disk. Thus a 2-dimensional manifold is a surface which at each of its points one can find a (possibly) small set topologically equivalent (homeomorphic) to an open circular disk at that point.
A set X is topologically equivalent, homeomorphic, to a set Y, if there is a one-to-one onto function from X to Y which is continuous and whose inverse function is continuous. From a topological point of view a square, a 5-pointed star, an ellipse, and a Euclidean circle are topologically equivalent. Note that some of these are smooth curves and some of them have corners. Some describe topology as rubber sheet geometry; sets are topologically equivalent if one can be transformed to another without cutting or tearing. In short, homeomorphic is the technical term for "topologically equivalent."
When manifolds are studied, mathematicians seek theorems which try to understand their structure. Figure 1 shows a series of 2-manifolds. Around each point of any of these surfaces (each of which is bounded) there is a small set equivalent to a topological copy of the interior of a 2-dimensional circle. The pattern shown here is the number of holes in the surface. The surface in the middle has genus one because it has one hole. You probably can also figure out how you might connect up copies of the surfaces to the left to get the surfaces farther to the right.

Figure 1 (Surfaces with zero holes, one hole, etc. Image Courtesy of the Manifold Atlas Project.)
What are reasonable pieces to decompose surfaces into? Natural choices will depend on the dimension of the manifold--above we saw pieces of spheres and tori, the kind of manifold one is dealing with. There are connected, bounded, smooth (differentiable), and compact manifolds, as well as manifolds with boundary. All of these flavors are designed to capture special properties of particular types of surfaces. Figure 2 shows a surface known as a pair of pants embedded in 3-dimensional space.

Figure 2 (The surface known as a pair of pants shown in 3-dimensional space. Image courtesy of Wikipedia.)
However, one can also consider a pair of pants drawn in the plane as shown in Figure 3. Looking at the same "object" in different settings often provides helpful insights into general principles about how to piece together or decompose complex surfaces into parts with nice properties. Note that the red circles are not part of the surfaces in question. What would happen if we added the red circles to the surfaces? Is each point now the center of a topological circle? A topologist might want to look at how much variety a surface could have if it was pieced together from pieces for which the pieces are pairs of pants.
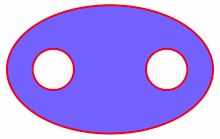
Figure 3 (A pair of pants drawn in the plane. Image courtesy of Wikipedia.)
Mathematics makes progress when things that seem to be identical can be told apart in some way. Thus, with time adjectives have been added to the term manifold to help tell different types of surfaces apart. So one talks of 2-manifolds, 3-manifolds, hyperbolic manifolds as well as other types mentioned above. Hyperbolic manifolds are those for which the area around each point looks like a hyperbolic space of some dimension. Spaces can be told apart in different ways, including using the notion of curvature. Euclidean spaces have zero curvature while hyperbolic spaces have negative curvature. In the Euclidean plane, thought of geometrically, given a point not on a line there is a single parallel through the point to the given line, while in the hyperbolic plane there will be many parallels to a given line through a point not on that line. Thurston investigated hyperbolic manifolds and spaces throughout his career.
Another complication with surfaces is the notion of orientability, a subtle idea having to do with whether or not one can maintain a consistent sense of direction on the surface. Figure 4 shows the famous Moebius strip (or band), which is not orientable. If you paste the short ends of a rectangle (say 2 inches by 12 inches) together you will get a part of a cylinder surface, which is an orientable 2-sided surface. If you give one of the short ends a half-twist and then paste them together, you get the Moebius strip, which is 1-sided and not orientable. Also, note that unlike the sphere (Figure 1, on the left) this surface has an "edge."

Figure 4 (The non-orientable surface known as the Moebius strip (band). Image courtesy of Wikipedia.)
Figure 5 shows the famous surface known as the Klein Bottle, for its discoverer Felix Klein. The Klein bottle is not orientable and furthermore it can't be embedded in 3-dimensional space without self-intersections, unlike the Moebius band which can be embedded in 3-space.
Figure 5 (Drawing of a Klein bottle. Image courtesy of Wikipedia.)
The diagram of the 2-manifold in Figure 6 shows an example of a much studied geometric object, the real projective plane, which can't be embedded into 3-space without self-intersections. The real projective plane is a structure where points and lines are defined with the property that any two distinct lines must intersect at a point. (The three basic types of plane geometry are Euclidean geometry, hyperbolic geometry (also known as Bolyai-Lobachevsky geometry), and the real projective plane.)
Figure 6 (Diagram of the real projective plane. Image courtesy of Wikipedia.)
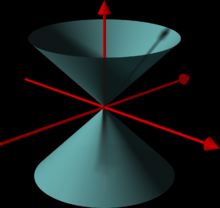
Having seen some different examples of surfaces that are 3-manifolds, it may be helpful to see an example which is not a manifold. Figure 7 show the two nappes of a cone which meet at the point where the three red lines meet. At that single point the surface fails to have an open Euclidean ball centered at that point which lies on the surface. All the other points are fine! (Note that each of the nappes of the cone separately are 2-manifolds.)
Figure 7 (A surface which is not a manifold. Image courtesy of Wikipedia.)
By the way, one can also talk about 1-manifolds. Thus, a circle or an open line segment in a plane will be 1-manifolds. However, the symbol for the number 8 or the infinity symbol will not be 1-manifolds because at the self-intersection point these two sets are not locally like open 1-dimensional balls.
Comments?
The Poincaré Conjecture
How can one recognize a topological 2-dimensional Euclidean circle? A basic property of topological circles is that they divide the plane into three sets: those points which are on the topological circle, those in the interior of the circle and those in the exterior of the circle. It seems so clear that simple closed curves, another name for a topological circle, obey this property that for many years no proof that this was true based on more basic geometric ideas had been provided. However, this step was taken by the French mathematician Camille Jordan (1838-1922); this result is known as the Jordan Curve Theorem. Simple closed curves are topological circles--homeomorphic to the Euclidean circle.
Photo of Camille Jordan
It is tempting to believe that it was easy to generalize ideas about topological circles to surfaces that are homeomorphic to the surface of a sphere in 3-dimensional space. However, mathematicians were coming to realize that the transition between properties of figures between spaces of different dimensions was not always easy. Thus, it turns out that if one has two simple polygons (the only places the sides of the polygons meet is at a vertex) of the same area, then one can cut up one of the polygons into a finite number of simple convex polygonal pieces and reassemble these pieces to form the other polygon, as if one had a jigsaw puzzle to solve. However, one of Hilbert's students, Max Dehn (1878-1952), who also made important contributions to the theory of surfaces, showed that the 3-dimensional analog of this theorem was false. Thus, it is not possible to take a cube and cut it into a finite number of convex polyhedral pieces and reassemble the pieces to form a regular tetrahedron of the same volume. Hence, mathematicians who were investigating the topology of manifolds and surfaces were cautious about transitions in dimension preserving what seemed like basic properties of 2-dimensional objects.
The French mathematician Henri Poincaré (1854-1912) was an early pioneer of looking at topological properties of surfaces. It was he who developed the important concepts of homotopy and homology that are basic ideas in modern topology.

Photo of Henri Poincaré
Poincaré tried to understand how varied the shapes that are topologically equivalent to higher dimensional spheres could be, in the same spirit that early workers in topology tried to understand how varied a shape which was in "essence" a simple closed curve could be. Poincaré thought about this question, now known as the Poincaré Conjecture, but did not actually state whether he thought the statement was true or false! In modern terminology, and in English (Poincaré wrote in French) the Poincaré Conjecture asserts:
If M is a closed simply connected 3-manifold, then M is homeomorphic to the 3-sphere.
Many topologists were inspired by the intuitive statement of this conjecture to work on this problem, and more generally to develop tools about manifolds that might help in answering the question one way or the other. Important mathematical progress in topology occurred because this seemingly simple question provoked interest. Thurston, in work that evolved after his doctoral work, became interested in all kinds of manifolds, in particular hyperbolic manifolds. The basic idea here is that at each point of the manifold it looks like a hyperbolic geometry space in some dimension. Over a period of time Thurston developed what has come to be called the Thurston Geometrization Conjecture. The intuitive idea is that any closed 3-manifold can be decomposed or broken up into pieces which are one of 8 types, which Thurston explicitly described and studied. The remarkable aspect of this conjecture was that if it could be shown to be true, then the Poincaré Conjecture would be a consequence.
Thurston and others showed that various special cases of the Geometrization Conjecture were true. In particular, Using very innovative ideas Thurston showed it was true of a rich class of manifolds known as Haken Manifolds. Haken Manifolds are named for Wolfgang Haken (1928- ) who is most famous for his work with Kenneth Appel showing that the 4-color conjecture is true.
Approximately at the turn of the 19th to 20th century David Hilbert (1862-1943) had collected and promoted interest in a collection of problems known as the Hilbert Problems whose solutions he felt would spur progress in mathematics. He was right! Many of these problems have been solved and resulted in lots of new mathematical ideas, and some of them are still being worked on. In the year 2000 a smaller collection of problems were formulated as the Millennium Problems, with the added carrot that obtaining an accepted solution of any of these problems carried with it a million dollar prize! One of the Millennium Problems was the Poincaré Conjecture.
In 2002 Grigori Perelman (1966- ) circulated a series of papers in which he claimed to have shown that the Poincaré Conjecture was true. His approach to the problem was to prove Thurston's Geometrization Conjecture. Not surprisingly his proof was subject to great scrutiny but in due course it was confirmed that what he had done was highly original and correct. The initial approach in Perelman's work has been expanded and improved upon, as is common after a breakthrough in proof methodology is found. When it was decided that his proof was right he was awarded the Millennium Prize which he refused to accept! He was also selected as one of the Fields Medal winners for 2006 (with Andrei Okounkov, Terrence Tao, and Wendelin Werner) but turned it down as well. The methods used by Perelman were based in part on ideas of Richard Hamilton on what has come to be called the Ricci Flow.

Photo of Grigori Perelman
Thurston's influence in mathematics and education
Some composers are short-lived and very prolific like Mozart, and some are prolific and long-lived like Franz Joseph Haydn. Yet no one doubts the importance and genius of Johannes Brahms despite an output of music much smaller than that of Mozart or Haydn. MathSciNet® is operated by the American Mathematical Society as a service to scholars around the world in abstracting and reviewing the publication of mathematical results. Not all of a scholar's output will be found there. For example, textbook and expository writing, lecture notes, etc. are not always reported on. MathSciNet lists 72 publications for William Thurston (and 4 for Bill Thurston) and indicates that in its database these publications have been cited 4338 times (as of late March 2017). In addition to all of the students he taught over his career he supervised the doctoral dissertations of 35 individuals, and the Mathematics Genealogy Project lists Thurston as having 222 descendants (as of March 2017). His son Dylan Thurston also has a doctorate degree in mathematics.
Thurston's mathematics pioneered the development of new approaches to exploring the interface of geometry and topology. There were those who were not fully comfortable with the less "formal" patterns that were emerging at the forefront of geometry and topology.
In a widely discussed article, "Theoretical Mathematics": Toward A Cultural Synthesis of Mathematics and Theoretical Physics" in the Bulletin of the American Mathematical Society, Arthur Jaffe (Harvard) and Frank Quinn (Virginia Technological University) commented on some new styles of doing mathematics and mathematical physics. Their note included this comment:
"William Thurston's 'geometrization theorem' concerning structures on Haken three-manifolds is another often-cited example. A grand insight delivered with beautiful but insufficient hints, the proof was never fully published. For many investigators this unredeemed claim became a roadblock rather than an inspiration."
Jaffe and Quinn were troubled by a "trend" to do more "experimental" work in mathematics and physics, and, in particular, to develop ideas that were concerned with physics but could not be tested using experiments nor, in their view, was this mathematical work subjected to the standards of "proof" that were used in more established parts of mathematics.
In the area of computer science it is common to hear the work of particular individuals as being in theoretical computer science. While often doing computer science involves the programming of computers (writing computer code) to carry out desired tasks, many individuals typically do not write code. Thus, while computers are programmed to carry out the task of sorting large lists of strings or of numbers, some computer scientists study sorting algorithms. Here the goal is to determine what is the best time or space complexity for any sorting algorithm or a specialized sorting algorithm for strings, perhaps one where all the strings are known never to involve more than 4 symbols (DNA sequences).
I have always liked the use of the phrase theoretical computer science and I have tried to use the phrase "theoretical mathematics" instead of the popular term used in mathematics, "pure mathematics." I have never been exactly sure what "impure mathematics" might be but there were always hints in my mind that people viewed work in "pure mathematics" as more valuable than in "applied mathematics." Mathematicians have certainly always drawn on subjects outside of mathematics (economics, physics, biology, chemistry, etc.) for inspiration. Many parts of applied mathematics deal with the theory of mathematical ideas which have proved of use in areas outside of mathematics and which have come to be studied for their own sake within mathematics. Thus, partial differential equations are used with great success in areas outside of mathematics but the existence and uniqueness of some kinds of partial differential equations are studied even when these equations are not used for any particular "applications."
Both the usefulness of mathematics outside of the field and the growth of mathematics itself are benefited by these studies. Jaffe and Quinn don't define "theoretical mathematics" but seem to use this term for theory that is not well rooted in the tradition that the ultimate goal of mathematics is to prove theorems. While I don't disagree that proving theorems is important, before one can in some cases prove theorems it is necessary to explore new ideas in a more flexible way until the ramifications of the new ideas and concepts gel in a way that supports the goal of providing proofs. Dynamical systems is an example of an area now firmly within mathematics where such experimentation was helpful in the development of the field. Bill Thurston was expert in finding new pathways to new conjectures and new proofs in geometric topology.
Many people responded to Jaffe and Quinn including Thurston himself. This whole discussion makes very worthwhile reading because it attempts to put in perspective what makes mathematics special as an academic discipline, how mathematics functions as a tool for other disciplines, and puts forth different views about how mathematics evolves and grows.

Photo of Bill Thurston
Comments?
My close encounter with William Thurston
While geometry has the appeal that it is quick-starting compared with other parts of mathematics because one can draw diagrams and work with physical models, the geometry that is taught in grades K-12 and even to undergraduates is quite limited and tends not to discuss recent developments in geometry nor does it deal with topics that current geometers think about. Thus, students typically learn about giving names to common shapes like cones, triangles, circles, and quadrilaterals and how to find the area and perimeter of simple geometric figures (triangle, circle). Students who major in mathematics in college, especially teachers often wind up taking a course, with a title like Euclidean and Non-Euclidean Geometry. Such courses are rooted in the development of geometry that grew out of Euclid's elements but take into account the "flaws" that are now understood to be present in this seminal work.
Many geometers find it frustrating that geometry courses are so rooted in ideas that are not what contemporary geometers think about. Thus, in 1990 I worked with Solomon Garfunkel, the executive director of COMAP, the Consortium for Mathematics and Its Applications, with funding from the Alfred Sloan Foundation, to have a group of research geometers and geometry educators meet to consider what might be suitable content for the undergraduate mathematics major survey course in geometry. Many people who did research in geometry or allied fields were invited to attend: Thomas Banchoff, Donald Crowe, Ronald Graham, Branko Grunbaum, Victor Klee, Walter Meyer, Marjorie Senachel and William Thurston. The discussions at this event and the position papers the attendees were encouraged to prepare appeared in the volume Geometry's Future that COMAP published.
The contribution that Bill Thurston provided was co-authored by John Conway and Peter Doyle, and in terms of pages, is the largest contribution to Geometry's Future. It involved notes for a course the authors had developed for students at Princeton University, who were not necessarily majoring in mathematics, which was taught using the title "Geometry and the Imagination."
This title harkens back to a book written jointly by David Hilbert and Stefan Cohn-Vossen (1902-1936) in 1932 based on notes that Hilbert had prepared for a course taught in 1921 called Anschauliche Geometrie. The English language version of this book appeared under the title Geometry and the Imagination, though this is certainly not a literal translation of the German (which can be rendered in a variety of different ways). The title Geometry and the Imagination represents well the spirit of what Hilbert and Cohn-Vossen wanted to do.

Photo of Stefan Emmanuilovich Cohn-Vossen
Cohn-Vossen had received his doctorate degree in 1924 under the direction of Adolph Knesser (whose son and grandson both became mathematicians) and had been working at Cologne University since 1930. In Germany then, as today, professors at German universities are government employees (civil servants) so when the Nazis promulgated their infamous racial laws (starting in about 1933) Cohn-Vossen lost his job. He left the country eventually going to Russia where he worked at universities in various cities. Sadly, in 1936 he died in Moscow of pneumonia.
David Hilbert is famous for his work on the foundations of geometry which he published in the book Grundlagen der Geometrie in 1899 and in 1905 in English under the title Foundations of Geometry. Hilbert had developed Euclidean geometry axiomatically using a collection of 21 axioms. It turned out though that one of these axioms could be proven on the basis of the others. However, Hilbert achieved the impressive accomplishment of showing that each of the 20 axioms was independent, that is for each axiom A, one could find a geometry where all the other axioms held except for A and where A did not hold. Hilbert's approach axiomatized Euclidean 3-dimensional geometry. It turns out that in 3-dimensional Euclidean geometry one can show that Desargues's Theorem holds in the planes of the geometry. However, if one looks at only plane geometry then there are examples of non-Desarguesian plane geometries (for example the Moulton plane). One can modify Hilbert's axioms by removing 4 of them to get an axiomatic system for plane Euclidean geometry.

Photo of David Hilbert
The Geometry and the Imagination notes of Conway, Thurston and Doyle are a very informative mathematical and educational document. They talk about an approach to actively engage students who already have an interest in mathematics as well as those who have "reservations" about mathematics. The notes are rich in suggestions of models for students to make, activities for them to try, and questions to think about. Examples are drawn from graph theory, knot theory, as well as more mainstream geometric topics. In addition to being in Geometry's Future these notes are also available in different incarnations on the Web. As a single sample of what is done, there is a discussion of thrackles, a notion invented by John Horton Conway. A thrackle is a special way to draw the diagram of certain graphs in the plane. While progress has been made on Conway's conjecture about the structure of thrackles, the question is still unsolved! Perhaps some student will find the answer based on looking at Geometry and the Imagination!
More Thurston
Let me mention two other truly remarkable contributions by Thurston to geometry. One of the ways Thurston generalized the notion of manifolds was by developing the idea of an orbifold. John Horton Conway, who was Thurston's colleague at Princeton, developed a useful notation for orbifolds which he used to investigate symmetry on various surfaces. Conway showed it was possible to explain the seemingly mysterious ad hoc facts that there are 7 types of friezes (see Figure 8 for sample friezes) on a Euclidean strip and 17 types of wallpaper patterns for the Euclidean plane.

Figure 8 (Two different types of frieze patterns. Image courtesy of Wikipedia.)
Conway achieved this using the orbifold concept and building on the idea of the Euler characteristic of a surface (for this case of the Euclidean plane). Thus, there is now a natural way of seeing where the numbers 7 and 17 come from!
In the study of manifolds it was often of interest to understand the ways that one could chop up a surface into triangles subject to various rules--ways to triangulate the surface. Triangulations of surfaces have turned out to have important applications in numerical analysis and in image processing (creating triangular meshes). Thurston looked at the interesting class of triangulation of a 2-dimensional sphere where there are exactly 12 vertices of valence (degree) five and all of the other vertices have valence 6. Branko Grünbaum and Theodore Motzkin had shown in the dual case (maps on the sphere with 12 pentagons and some number of hexagons, which have come to be known as fullerenes) that such triangulations exist for every possible value for the number of 6-valent vertices other than 1. Some also refer to fullerenes as Goldberg polyhedra; these polyhedra have received attention recently because of new discoveries of examples of such polyhedra with high levels of symmetry where all the edges have equal length. Thurston's discovery here was that there were surprisingly many inequivalent polyhedra with triangle faces having the positive integer number h 6-valent vertices and twelve 5-valent vertices, thus making them a rich collection of highly structured polyhedra to investigate. He described various ways of constructing these polyhedra.
Given Thurston's highly visual approach to doing and thinking about mathematics it is not surprising that some of what he did has been captured with videos, some of which he was involved with developing. One of these videos is a discussion of a construction that Thurston developed to show that it was possible to turn a sphere in three space inside out without creating any creases and pinching, a process known as eversion. The surprising fact that this is possible was first shown by Thurston's academic grandfather Stephen Smale. Here is the full video version of Thurston's idea in a film made at the now defunct Geometry Center. There is a nice video about knots, and another video where Thurston talks about knots.
As you enjoy Mathematics and Statistics Awareness Month, remember Bill Thurston!

Photo of Bill Thurston (Note the formula on his sweat shirt!)
Comments?
References
Atiyah, M. et al., Response to "Theoretical Mathematics toward a cultural synthesis of mathematics with theoretical physics, Bulletin of the American Mathematical Society, 30 (1994) 178-207.
Conway, J. and H. Burgiel, H., C. Goodman-Strauss, The Symmetry of Things, A K Peters Wellesley, MA, 2008.
Gromov, M. and W. Thurston, Pinching constants for hyperbolic manifolds, Invent. Math., 89 (1987) 1-12.
Gray, J., Henri Poincaré: A scientific biography. Princeton University Press, Princeton, 2012.
Grünbaum, B. and T. Motzkin, The number of hexagons and the simplicity of geodesics on certain polyhedra, Canad. J. Math. 15(1963) 744-751.
Jaffe, A. and F. Quinn, "Theoretical Mathematics toward a cultural synthesis of mathematics with theoretical physics, Bulletin of the American Mathematical Society, 29 (1993) 1-13.
Malkevitch, J. (ed.), Geometry's Future (2nd. edition), COMAP, Bedford, MA, 1991.
Thurston, W., Three-dimensional manifolds, Kleinian groups and hyperbolic geometry, Bull. Amer. Math. Soc. 6 (1982) 357–381.
Thurston, W., Hyperbolic structures on 3-manifolds. I. Deformation of acylindrical manifolds. Annals of Math., 124 (1986), 203–246.
Thurston, W., On the geometry and dynamics of diffeomorphisms of surfaces. Bull. Amer. Math. Soc., 19 (1988), 417–431.
Thurston, W., Mathematical education, Notice of the American Mathematical Society, 37 (1990) 844-850.
Thurston, W., On proof and progress in mathematics, Bulletin American Mathematical Society, 30 (1994) 161-177.
Thurston, W. and S. Levy (ed.), Three-dimensional geometry and topology. Vol. 1. Princeton University Press, Princeton, 1997. (Thurston had privately distributed various versions of his writing and course notes on manifolds. His student Silvio Levy worked with Thurston on turning these notes into this volume.)
Schein, S. and J. Gaye, Fourth class of convex equilateral polyhedron with polyhedral symmetry related to fullerenes and viruses, Proceedings of the National Academy of Sciences, 111 (2014) 2920-2925.
Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet® can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be found via the ACM Portal, which also provides bibliographic services.
 Joseph Malkevitch
Joseph Malkevitch
York College (CUNY)
Email Joseph Malkevitch


 Joseph Malkevitch
Joseph Malkevitch