The Princess of Polytopia: Alicia Boole Stott and the 120-cell
Posted October 2006.
Alicia Boole Stott's first article, On certain series of sections of the regular four-dimensional hypersolids, published in 1900, is the basis for this month's feature column...
Tony Phillips
Stony Brook University
tony at math.sunysb.edu

Fig. 1. A reconstruction of seven of Alicia Boole Stott's models showing 3-dimensional slices of the 120-cell. These slices go from the bottom to the midpoint; then the first six would repeat in reverse order. Photograph by Tony Scarlatos, Stony Brook.
A paradoxical childhood and an unusual hobby
Alicia Boole (1860-1940) grew up in the highest intellectual circles of Victorian England, and in deep penury. Her geneaology was excellent: Boolean Algebra and Mount Everest are named, one for her father George Boole and the other for her maternal uncle, Sir George Everest. But Boole married late and died young, leaving his wife Mary with five daughters, the eldest eight, the youngest six months old, and no money. Alicia, four at the time, was sent to live with relatives. When she rejoined her family they were living "in a poor, dark, dirty, uncomfortable lodging in Marylebone" according to H. S. M. Coxeter, who collaborated with her much later and who contributed a short biography to "Women of Mathematics."
In London the girls, especially the younger, received little or no formal education. Alicia is said to have learned the first two books of Euclid, and no more. But Mary Boole, who corresponded with Darwin and was friends with H. G. Wells, received many visitors, guests who could keep the family acquainted with developments in science and society (or at least those on the mystical fringes of both: Coxeter characterizes them as "a continual stream of cranks"). One of the cranks had a son named Howard Hinton, a brilliant polymath, who courted and married the eldest of the Boole daughters. Hinton was fascinated by four-dimensional geometry. He brought over an elaborate system of wooden cubes he had designed to make it comprehensible, and set his fiancée's younger sisters to work on them. Alicia, then around 18, "gradually began to surpass him in her ability to understand what happens in hyperspace" (Coxeter). She worked out by herself the six regular polytopes (the 4D analogues of our regular polyhedra) and built cardboard models of their sections by parallel 3-planes.
Alicia was building her models just before Edwin A. Abbott's book "Flatland" appeared (1880) and before W. I. Stringham published Regular figures in n-dimensional space in the American Journal of Mathematics (also 1880), but she considered her research her own private hobby. Only towards the end of the century, when her husband (she had married Walter Stott in 1890) showed her that figures published by the Dutch geometer Pieter Schoute closely resembled her own constructions, did she contact a professional mathematician. Schoute became her enthusiastic supporter, and arranged for the publication of her diagrams in the proceedings of the Royal (Netherlands) Academy of Science.
Alicia Boole Stott's first article, On certain series of sections of the regular four-dimensional hypersolids, published in 1900, is the basis for this month's feature column. We will focus on her analysis of one of the "hypersolids," the 120-cell, with boundary consisting of 120 dodecahedra. In particular we will show how to use her diagrams as templates to reconstruct seven of the polyhedral models she had built some twenty years before.
Alicia left Schoute with a complete set of models for the 120-cell and its dual, the 600-cell; these are still on display at the University of Groningen, where Schoute taught, and can be seen as part of Groningen's online display of Mathematical models of surfaces.
Another set of her models is on exhibit at The Faulkes Institute for Geometry, Centre for Mathematical Sciences, Cambridge University. The Cambridge set duplicates most of the two series of 600-cell sections at Groningen (some with different color-coding), but comes with a different set of drawings. Cambridge does not seem to have any models of the 120-cell sections.
A Flatlander's views of the dodecahedron
A 120-cell is sitting in x, y, z, w-space with one of its dodecahedral faces in the 3-plane {w = 0}, and the rest of it in the "upper" half-space where w > 0. Alicia Stott examined its sections by 3-planes {w = c}, parallel to the x, y, z-plane, as c increases from 0 to the height of the 120-cell, approximately 6 units if the dodecahedra have edge length 1. These sections are what would appear if a 120-cell traveled "downwards" on a path intersecting the space we live in.
"Flatland" explains this process by analogy with a 2-dimensional being's perception of a 3-dimensional solid. All the Flatlander can see is the sequence of planar figures produced as the solid drops through Flatland. It is a useful exercise to imagine how a Flatlander would see a dodecahedron passing face-first, vertex-first or edge-first, because the three families of polygons produced are exactly those we will encounter in Alicia's models.
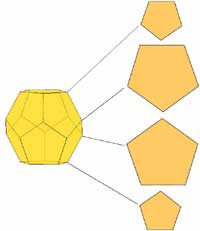
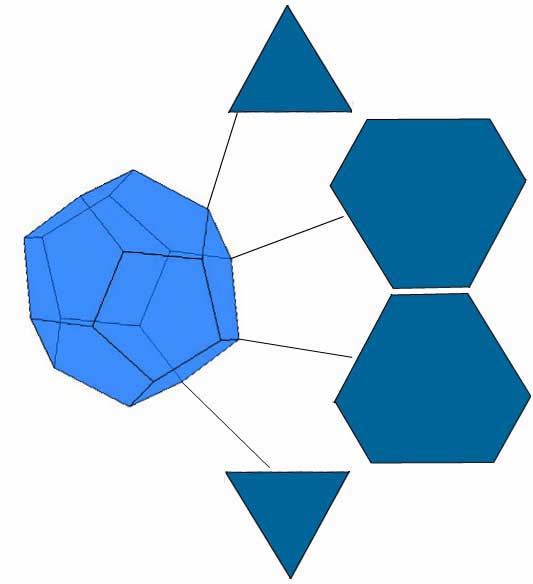
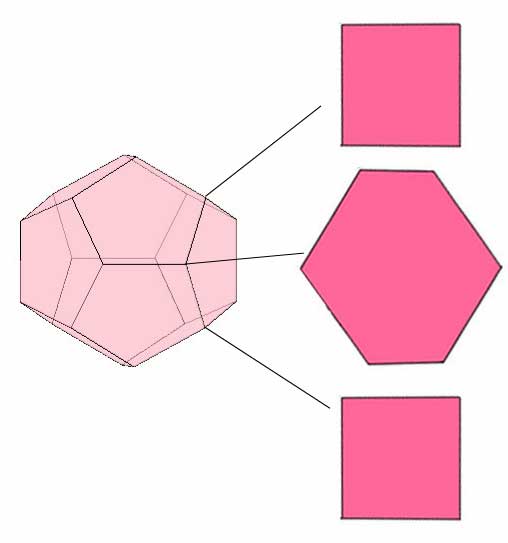
Fig. 2. Three Flatland perspectives on the dodecahedron.
- Slices parallel to a face. The vertices are encountered in four groups of 5. As the slices move up, the pentagonal intersection grows. Between the two middle sets of vertices, the slices are decagons (not shown), with a regular decagon at the midpoint. Then another family of pentagons, rotated with respect to the first, decreasing to the top face.
- Slices perpendicular to a diameter joining opposite vertices. The vertices are encountered, in groups of 1, 3, 6, 6, 3, 1, at six levels. Between level 1 and level 2, the sections are equilateral triangles. Between level 2 and level 3, the sections are hexagons, with a regular hexagon (not shown) occurring along the way. Between the middle levels, the hexagons change shape, with another, larger, regular hexagon at the very center. The process reverses as we slice towards the top: hexagons and then triangles.
- Slices perpendicular to the bisector of two opposite edges. Now the vertices are encountered 2, 4, 2, 4, 2, 4, 2 at seven levels. The first slices are very thin rectangles, becoming a perfect square at level 2. Between levels 2 and 3 the slices are octagons (not shown). Then hexagons between levels 3 and 5, with a regular hexagon appearing once between 3 and 4, and again between 4 and 5 (not shown). The first steps then reverse: octagons, square, rectangles diminishing to a line segment.
The 120-cell sits for its picture
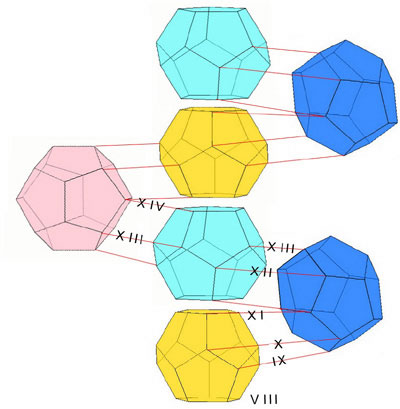
Fig. 3. The 120 dodecahedra constituting the 3-dimensional boundary of the 120-cell can be analyzed into 9 layers containing 1, 12, 20, 12, 30, 12, 20, 12, 1 solids respctively. This picture illustrates how the layers stack up when the polytope is placed with one solid face in x, y, z-space. One representative is shown from each layer, with indications of how the layers are attached. In this orientation of the polytope the top and bottom cells have no 4th-dimensional extent. They appear here as the bottom yellow pentagon and the top turquoise pentagon. Roman numerals refer to diagrams in Alicia Boole Stott's 1900 paper.
Up through the layers
The models in this sequence were assembled with the help of George Hart, Lucienne Pereira and Steven Anderson. They were photographed by Tony Scarlatos. The images from Stringham's paper were photographed by Bill Casselman. The templates from which the models were made were photographed by Robert Sammis from the fragile fold-out plates attached to Stott's article. Thanks to all!
 |
Layer 1. Alicia's diagrams give us a 3-dimensional perspective on the 120-cell, analogous to the first (yellow) Flatland picture, where one face is in the inhabited plane. The first thing the Flatlander sees is that face. The first thing we see is a single, entire dodecahedron popping into view. We can think of its skin as formed by the twelve bottom pentagons of the Layer-2 solids, and color it yellow. Assembled from Stott's Diagram VIII.
|
 |
Layer 2 consists of twelve dodecahedra attached to the twelve faces of Layer 1. As we move up through Layer 2, each dodecahedron gives larger and larger pentagons. This model shows the largest, just before we encounter the first trace of Layer 3. Assembled from Stott's Diagram IX.
The image on the right is Fig. 18 from Stringham's 1880 American Journal paper. It shows all of Layer 2, before the Layer 3 polyhedra have been added. Stringham projected the entire construction into 3-space, which distorts the geometry but makes the organization intelligible.
|
 |
 |
Layers 2 and 3. This model is assembled from Stott's Diagram X. One Layer 3 dodecahedron is inserted vertex-first into each of the 20 dimples shown in Stringham's Fig. 18. In this section, each of these polyhedra contributes a triangle.
|
 |
The top of Layer 2; Layer 3. From Stott's Diagram XI. This is the last we will see of Layer 2. Each of the twelve shows its top face before disappearing. The Layer 3 polyhedra are now contributing hexagons.
On the right is Stringham's Fig. 19. It shows how the Layer 3 polyhedra form pentagonal pits. (At the bottom of each pit is the top face of one of the level-2 dodecahedra)
|
 |
 |
Layers 3 and 4. From Stott's Diagram XII. One (turquoise-colored) dodecahedron is plugged into each of the 12 pits shown in Stringham's Fig. 19. These new solids are stacked directly on top of the Layer 2 doecahedra and will also give pentagonal sections.
Stringham's Fig. 20, on the right, shows how the tops of the Layer 4 dodecahedra form 12 plateaus, while the tops of the Layer 3 dodecahedra appear as 20 triangular peaks. The sides of the plateaus and the peaks form a network of 30 four-sided troughs.
|
 |
 |
Layers 3, 4 and 5. One (pink) Layer-5 dodecahedron is inserted edge-first into each trough. In this section, assembled from Stott's Diagram XIII, it contributes a square. The Layer-3 dodecahedra make their last appearance as triangles, while those in Layer-4 continue to contribute pentagons.
|
 |
Layers 4 and 5. In this section, from Stott's Diagram XIV, each Layer-4 dodecahedron shows its top face, while each of the 30 Layer-5 docecahedra contributes its central section. This is the half-way point of the slicing process: we have seen 1 + 12 + 20 + 12= 45 full dodecahedra and half of 30 others. As we contine to move up thrugh the 120-cell, the sections will now become smaller. We could use the same models in reverse order, except yellow and turquoise would need to be interchanged to follow the color scheme of Fig. 3.
Stringham's Fig. 21 (at right) gives a different perspective on the end of the process. In his figure the entire Layer 5 has been added. Each trough has been transformed into a 4-sided ridge; the Layer-5 polyhedra enclose 12 pits (at the bottom of them you can see the last pentagons from Layer 4); and three by three they form 20 dimples. This solid contains 75 dodecahedra, with surface geometry the exact opposite of the 45-dodecahedron solid shown in his Fig. 20. Locally it is clear how the two solids mesh together perfectly: dimple to peak, pit to plateau and ridge to trough. Globally this matching, which produces a topological 3-sphere, cannot be carried out in our world.
|
 |
The templates
Alicia Boole Stott's 1900 article in the Royal Netherlands Proceedings has 14 diagrams illustrating polygonal configurations; the first seven relate to sections of the 600-cell, and the last seven, numbered VIII to XIV, relate to the 120-cell. These diagrams can be used as templates to assemble models exactly like the ones she made herself and left in Groningen. The only difference is that the Groningen series includes several intermediate sections for which she did not publish diagrams. These diagrams are all exactly to the same scale. They are published in black and white, but I have followed the example of her actual models in color-coding by layer.

Diagrams VIII and IX

Diagram X
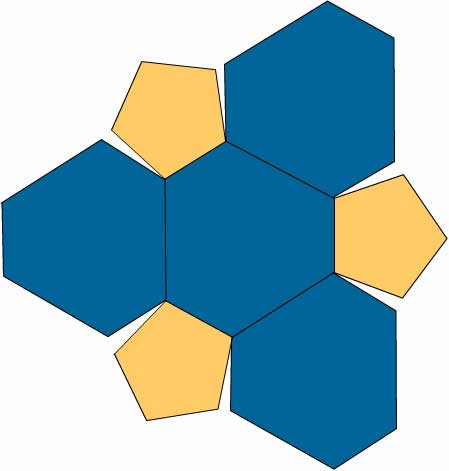
Diagram XI

Diagram XII
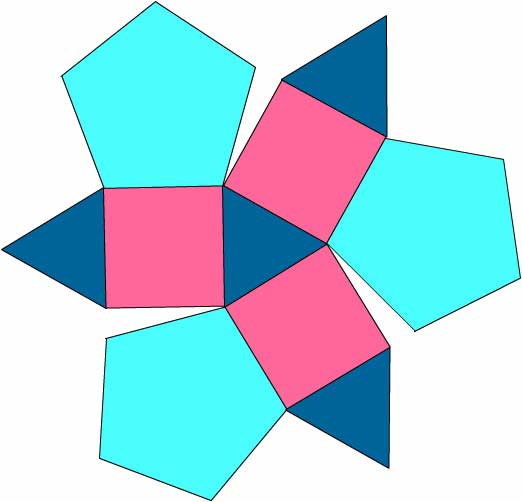
Diagram XIII
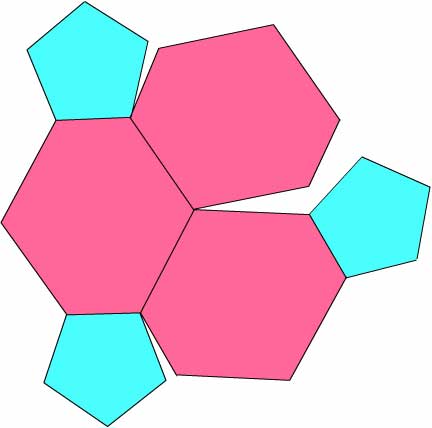
Diagram XIV

The assembly of Diagram XIV. Note the George Hart method of double tabs, Elmer's glue applied with a brush, and clips.
For further reading ...
Coxeter's biography of Alicia Boole Stott appears in
- Grinstein, Louise and Paul J. Campbell, eds., Women of Mathematics: A Biographical Sourcebook, Greenwood Press, Westport CT 1987.
He wrote her a shorter but more personal biographical notice, and of course everything you need to know about the 120-cell, in
- Coxeter, H.S.M., Regular Polytopes, Dover, New York, 1973.
There is more material about Alicia and her brilliant, eccentric family in
- MacHale, Desmond, George Boole: His Life and Work, Boole Press, Dublin 1985.
and in her nephew Sir Geoffrey Ingram Taylor's "Scientific Diversions," published on pp. 137-148 in
- Higginbotham, S. W., ed., Man, Science, Learning and Education, Rice University Studies LXIX supplement 2, 1963.
[Added 05/09:] A recent survey of Alicia's life and mathematical contributions:
- Irene Polo-Blanco, Alicia Boole Stott, a geometer in higher dimension, Historia Mathematica 35:2 (May 2008) 123-139.
For a more systematic treatment of the problem of slicing convex bodies in n-space, see Hermann Weyl's The elementary theory of convex polyhedra in
- Tucker, A. W. and Harold Kuhn, Contributions to the Theory of Games, Vol. I, Annals of Mathematics Studies #24, Princeton 1950.
Full references for the articles referred to in the text are:
- Stringham, W. I., Regular figures in n-dimensional space, Amer. Jour. Math. 3 1880 1-14.
- Stott, Alicia Boole, On certain series of sections of the regular four-dimensional hypersolids, Verhandelingen der Koninklijke Akademie van Wetenschappen te Amsterdam (eerste sectie) 1900.
Tony Phillips
Stony Brook University
tony at math.sunysb.edu
NOTE: Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal, which also provides bibliographic services.




























