cusp2 The Catastrophe Machine
2. An algebraic version of the double well
It is awkward to calculate precisely the angle at which the catastrophe happens in the double-well example. There is a more algebraic version of the phenomenon which is easier to work with.
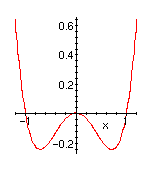 | Imagine that the ball is constrained to roll on the graph of the function y=x4-x2. Instead of tilting the graph we perturb the function by adding a linear term (ax) so as to raise one well and lower the the other. |
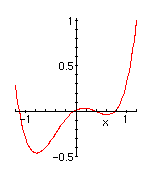 | a=0.3 Here is the graph of y=x4-x2+.3x. If the ball had started on the right, it would still be on the right. |
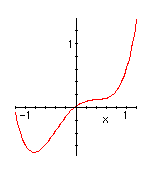 | a=0.6 Here is the graph of y=x4-x2+.6x. The ball would have rolled over to the left. The exact point at which this happens can be reckoned (easy calculus exercise) to be a=(4/3)*(1/6)1/2=.5443... |
The corresponding negative values a=-.3, a=-.6 give graphs where the left well grows higher than the right. These values and the initial a=0 generate a family of figures exactly analogous to the the configurations 1 -- 9 of our original double well. The perturbation parameter a plays the role of the angle of tilt.
The catastrophes take place when a=(4/3)*(1/6)1/2 and when x=(1/6)1/2=0.4082... Looking closely at the graphs right near the catastrophe point, for values of a just above and just below the critical value a0=.5443..:
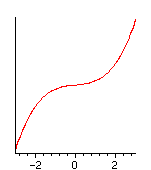
a=a0+0.00001
|
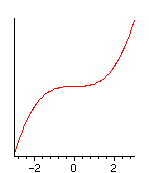
a=a0
|
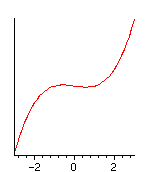
a=a0-0.00001
|
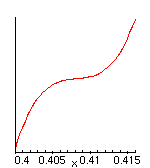 | 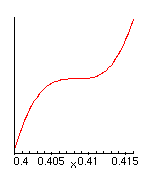 | 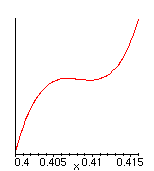 |
makes it plausible that the graph can be reparametrized near the catastrophe point as y=x^3, and that this catastrophe can be explained mathematically as a perturbation of the function y=x^3 so as to create, or destroy, a local minimum near x=0.
Here we can see the reason for the name "Fold Catastrophe." If the graph is projected onto the y-axis, the catastrophe corresponds to the appearance or disappearance of a pair of folds.