All for Nought
Posted February 2007.
By accident, it records the oldest "0" in India for which one can assign a definite date...
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
The history of zero is a bit complicated. So is the history of "0". The scholarly literature on the subject is only tentative because much of the historical record is very sparse, whereas the popular literature is unfortunately and frequently both confident and in error.
The first problem to come along is deciding exactly what one means by "zero" or, for that matter, "0". Is it a number in the mathematical sense - that is to say, the cardinality of the empty set? The length of a point? The result of subtracting 1 from 1? I am not going to engage in such deep matters, but rather in a much more pedestrian business. The digit "0" was a basic part of decimal place value notation. There is no doubt that it was invented in India, but exactly how and for what purpose is unclear, and probably always will be.
This is not at first sight very complicated mathematics, but in truth it took far longer for humans to develop a convenient notation for calculating than it did for them to develop rigourous mathematical reasoning. The apparent simplicity of our current system is indeed a sign of its elegance. It often happens that the best mathematics, once seen, is seen to be obvious.
I'm going to cover a very small part of the story.
Mathematical tourism
|
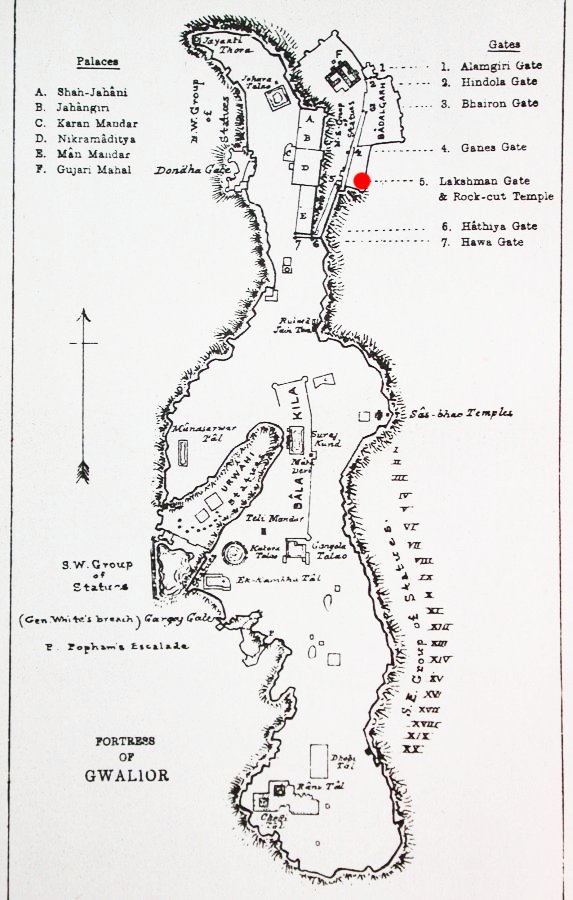
The city of Gwalior in India is located on the main rail line south from Delhi, just a bit below Agra, the site of the Taj Mahal. It is in the far north of Madyha Pradesh, and lies very near where the three northern states of Rajasthan, Uttar Pradesh, and Madhya Pradesh meet. It is in a region that has few hills and - for most of the year, like much of India - little water.
Gwalior does not seem to be well known outside India, although it is certainly mentioned favourably in guide books. The reason for this favourable mention is that it happens to be the site of one of the most impressive of all medieval forts in a country full of impressive forts. The fort is famous inside the country not only for its size and beauty, but also for being the site of the last and futile stand of the Princess (Rani) of Jhansi during the rising of 1857-1858 against the British.
|
|
 From an appendix in Cunningham's Reports
From an appendix in Cunningham's Reports |
The city is now both sprawling and crowded, with a population of perhaps 2,000,000, but until recently it was relatively small, and designed to be small.
The fort occupies a plateau in what is now the center of the city, but was once on its western boundary. The plateau is about 300 feet high built of basalt, rising steeply from the plain below. It is a bit less than two miles in length from north to south, maybe an average of a half mile from west to east.
The site is of mathematical interest because of what is written on a tablet recording the establishment of a small 9th century Hindu temple on the eastern side of the plateau (marked by the  on the nineteenth century map at the left). By accident, it records the oldest "0" in India for which one can assign a definite date. on the nineteenth century map at the left). By accident, it records the oldest "0" in India for which one can assign a definite date.
|
The temple
|
The temple is dated to 876 A. D. and is much older than the current fort, whose construction was begun in the late 15th century, although it was built quite a while after the original one constructed on the plateau. It is, like many temples in India, monolithic - that is to say, originally carved out of one single chunk of stone. It was dedicated to Vishnu, but is no longer an active site of worship.
|
|
|
|
The temple is named Chatur-bhuja, that of the four-armed god. Who was reponsible for the (literal) defacement of the statue is not known to me.
|
The tablet
|
Just inside the inner chamber, on Vishnu's right hand side, is the dedication tablet. The tablet records the date (in the local era, which started in 57 B. C.), the dimension of a land grant to a neighbouring temple, and the size of a daily gift of flowers to be paid for from an endowment made to this temple.
|
 |
What is surprising about these numbers is that they are so similar to what modern civilization uses currently. The more you learn about how our current number symbols developed - transmitted from the Hindus to the Persians, then to Mediterranean Islam, and differently in East and West - the more remarkable this appears. Here, for comparison, are some numbers from the bus system of Mumbai:


Photographs taken by Leslie Saper
Go figure.
The background
What the Gwalior tablet shows is that by 876 A. D. our current place-value system with a base of 10 had become part of popular culture in at least one region of India.
We know almost nothing of how this decimal place-value notation came about, although there are many suggestive facts. One feature of Hindu culture in the middle centuries of the first millennium was that its texts were largely in verse, and preserved through oral tradition. It is hard to fit a useful numerical notation into such a scheme, and in fact what we see is a large literature, written down only much later than it originated, with numbers - often very, very large numbers - written in a kind of decimal place-value notation, but in words instead of symbols. Furthermore, the demands of the metric of the verses required that the exact words chosen to represent a given digit might vary from one point to another, so as to scan correctly. Whether this usage overlay more convenient calculation with symbols is not known to us, although it is almost inconceivable that it did not.
Another problem is that the climate of India is harsh. Paper was introduced to India late, and until then the materials on which things were written were birch bark in the north and palm leaves in the south. These are both extremely fragile. There are many extant manuscripts written on these, but nearly all of relatively recent date.
One of the more intriguing questions about the origin of decimal place-value notation is what connection it had to a much older tradition from a nearby region. The Babylonians began writing in about 3000 B.C., and had the good fortune to write on clay tablets, which can last for a very long time. We have extensive records from several thousand years of their development. They used an extremely sophisticated place-value system, remarkably much the one we use today, from very roughly 2000 B.C. on, but with a base of 60 instead of 10, and without "0". All the evidence that I am aware of suggests that this was technology acquired only by an elite group through rigourous training. This somewhat ambiguous notation persisted to about 300 B.C. when Babylonian astronomical tables started to incorporate a symbol that to some extent performed as zero, that is to say as a sign to indicate a space between two "digits". This was adopted in modified form by Greek astronomers after the conquests of Alexander, and this science in turn was transmitted (along with astrology!) to India sometime in the first few centuries of the current era. Exactly how these transmissions occurred is lost to us.
References
Section XVI of volume II contains the only substantial history of the city and principality of Gwalior that I have been able to locate. Cunningham mentions the temple and the tablet as well as its date 933, but does not mention the other numbers.
There are two inscriptions in the temple at Gwalior, one just above the entrance in a small domed porch, and the other on the left inside wall. The first is, as Hultsch says, written in a more attractive style (and, he also says, a more stylish Sanskrit), but has no mathematical interest, contrary to what is sometimes said.
Hultsch's article contains a transcription of the tablet into modern Sanskrit script, an English translation, and a reproduction of a rubbing of the tablet. Aside from the numerals, the tablet does not seem to be of much historical interest.
This book is useful, perhaps even indispensable, for someone interested in the history of numbers. It is a huge compendium of material, some fascinating and much - alas - of very little interest. One problem is that the author fails to warn you when he is relying on secondary material and when on first hand. This problem actually arises in his account of the temple of Gwalior - he has apparently misread Hultsch's transliteration and thought that the numbering of the Sanskrit verses found there was part of the inscription. One very valuable feature of Ifrah's books is the extensive bibliography.
This book mentions Gwalior, but it is an uninteresting account, and seems to be passing on only third-hand information (as I have said, a frequent phenomnon in popular accounts of the history of science). I doubt that he has bothered to read Hultsch's article. but instead seems to rely principally on Ifrah. Even taking this into account, the sketches of the numerals at Gwalior have strangely little resemblance to the originals.
- Alexander Cunningham, Four reports made during the years 1862-63-64-65, Archaeological Survey of India, 1865.
- E. Hultsch, The two inscriptions of the Vaillabhattasvamin temple at Gwalior, Epigraphia Indica I, pages 154--161.
- George Ifrah, The universal history of numbers, Penguin, 2000.
- Robert Kaplan, The nothing that is, Oxford University Press, 1999.
- Shunya's collection of photographs of Gwalior will give you a good idea of the beauty of the fort as well as a look at the rest of the town. The eastern approach to the fort is shown in the image Pedestrian entrance, and the temple is just at the bend in the road at middle left.
Acknowledgements
Dipendra Prasad of the Tata Institute in Mumbai arranged my visit to Gwalior at very short notice, and in particular arranged for me to meet Renu Jain, head of the mathematics department at Jiwaji University in Gwalior. She, at even shorter notice, gathered a small group to guide me, among them V. P. Saxena (mathematics) and A. K. Singh (archaeology). I wish that I had had more time to talk with them about the history of Gwalior.
Images
Images by the author (mostly) and Leslie Saper. Personal use of the above images is allowed. Inquiries about publication of any of the above images should be sent to the AMS Public Awareness Office paoffice@ams.org.
Bill Casselman
University of British Columbia, Vancouver, Canada
cass at math.ubc.ca
NOTE: Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal, which also provides bibliographic services.







 on the nineteenth century map at the left). By accident, it records the oldest "0" in India for which one can assign a definite date.
on the nineteenth century map at the left). By accident, it records the oldest "0" in India for which one can assign a definite date.















