The Octosphericon and the Cretan Maze
Posted May 2006.
The Cretan Maze is an archetypical design -- it dates back some 5000 years...
Tony Phillips
Stony Brook University
tony at math.sunysb.edu
The octosphericon
The octosphericon is a generalization of C. J. Robert's sphericon (see also "The differential geometry of the sphericon" and "Cone with a twist"): the surface of the body obtained by rotating a square about one of its diagonals, slicing the resulting solid along a plane through the axis of rotation, rotating one of the halves 90o with respect to the other and reattaching the two.




Construction of the sphericon: a double cone is sliced, half gets rotated, and the halves are rejoined.
The (prime) octosphericon is constructed in the same way, but with an octagon instead of a square, and with a relative rotation of 45o instead of 90.

The octosphericon. A relative rotation of minus 45o between the two half spun-octagons would give a mirror-image surface. A relative rotation through 90o would give a different surface.
The Cretan maze
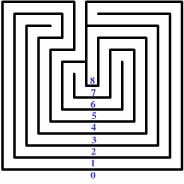
The Cretan maze is an archetypical design -- it dates back some 5000 years. On the island of Crete, it came to symbolize the Labyrinth in which the Minotaur was kept. The city of Knossos, where King Minos had his palace, used this design on coins between roughly 500 and 200 BC.

The Cretan maze can be drawn as a game: start with the "nucleus" on the left, join the lower central end to the one immediately on its right, and continue joining the next free end on the left (the dots count as ends) to the next free end on the right, always going around the bottom.
The level sequence of the Cretan maze
The Cretan maze is organized on 8 concentric levels. The path from the outside to the center traverses these levels in an order which is characteristic of the maze. If we number the levels 1 to 8, and represent the outside by 0, then following the path through the maze produces a sequence of numbers, starting with 0 and ending with 8: this is the level sequence of the maze.

The path from the outside to the center meets the numbers 0 3 2 1 4 7 6 5 8 in that order. This is the level sequence of the Cretan maze.
The Cretan maze is just one of a family of mazes which share three properties:
- A single path runs from the outside to the center.
- The maze is organized on concentric levels; the path traverses each level exactly once.
- The path changes direction each time it changes level.
Here, for example, are two others of the 42 eight-level mazes of this type:

Cretan-type mazes with level sequence 0 5 6 7 4 1 2 3 8 and 0 7 2 5 4 3 6 1 8.
Level sequences of Cretan-type mazes
For a permutation of the integers 0 through 8 to be the level sequence of a Cretan-type maze it must satisfy
- It starts with 0 and ends with 8.
- Odds and evens alternate.
- The number-line segments corresponding to an even integer and its (odd) successor in the permutation must obey the "no-overlap" law: if two of these segments intersect, one must be contained inside the other. Similarly the number-line segments corresponding to an odd integer and its (even) successor must also obey the "no-overlap" law.
For example, in the maze 0 5 6 7 4 1 2 3 8, the first set of number-line segments is [0,5], [6,7], [4,1], [2,3]; note that [2,3] is inside [4,1] which is inside [0,5], while [6,7] is disjoint from all of them.
Cretan-type mazes and chord diagrams
An n-chord diagram consists of 2n points on the perimeter of a circle, and n non-intersecting chords joining them. The "no overlap" condition for a level sequence of length 2n can be interpreted in terms of chord diagrams if we identify 0 and 2n. Then the n [odd, even] segments form an n-chord diagram, and the n [even, odd] segments form another.
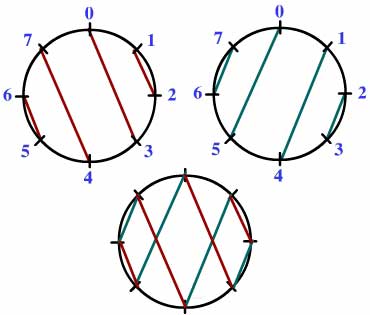
The two chord diagrams corresponding to the Cretan maze 0 3 2 1 4 7 6 5 8. Two chord diagrams give a Cretan-type maze if and only if they link to give a path visiting every vertex.
Chord diagrams on the octosphericon, the link to the Cretan maze
Each half of a spun octagon gives a chord diagram (in fact, in several different ways). Suppose we number the sides of the octagon from 0 to 7. Then rotating about the axis through the intersection of sides 1 and 2 creates a surface, each half of which contains a band linking sides 0 & 3, 2 & 1, 4 & 7, 6 & 5. If the half-surface is turned 45o leaving the octagon fixed, its bands now join sides 1 & 4, 3 & 2, 5 & 0, 7 & 6. When the two halves are joined to form the octosphericon, the surface forms one continuous band joining 0 3 2 1 4 7 6 5 8 in that order: the level sequence of the Cretan maze.

Rotating the octagon about the axis AA' produces bands in each half of the spun octagon. If the sides of the octagon are numbered 0 ... 7 as shown, the bands on the half-octosphericon join 0 to 3, 2 to 1, 4 to 7 and 6 to 5. The other half-octopshericon is rotated through 45o relative to the first. Its bands now join 1 to 4, 3 to 2, 5 to 0 and 7 to 6.
Make your own Cretan-maze octosphericon
An octosphericon may be constructed by joining two copies of this template. The photographs show how to attach tabs (for a paper model) and how to number the sides of the inscribed octagon. Good Luck!


The two halves, with numbers and tabs, for a paper model of the Octosphericon. Note that the tab placements are slightly different. I chose two different colors of construction paper to make the assembly more intelligible.

The Cretan Octosphericon partially assembled.



The final product.
For further reading ...
Hermann Kern, Through the Labyrinth: Designs and Meanings over 5,000 Years, Prestel, 2000. [The best and most complete resource on mazes and labyrinths].
Anthony Phillips, Topology of Labyrinths, in L'Occhio di Horus, Itinerari nell' Imaginario Matematico, M. Emmer, ed., Istituto della Enciclopedia Italiana, Rome 1989. [Exact definition of "cretan-type," proof that level sequence determines maze. This information is also available in Through Mazes to Mathematics].
Anthony Phillips, Meander mazes on polysphericons, in The Visual Mind II, M. Emmer, ed., MIT Press, 2005. [Has more general discussion and more templates].
Tony Phillips
Stony Brook University
tony at math.sunysb.edu
NOTE: Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal, which also provides bibliographic services.

















