orbits1 A new solution to the three body problem - and more
by Bill Casselman Feature Column Archive
NOTE: This month's column contains several Java applets. They may not work on your particular computer, for any of various reasons. If you do not have Java enabled in your browser, for example, you will see only static images representing the animated applets. If you have trouble with viewing the applets even though Java is enabled, or if you want to print out this note, you should disable Java. If Java is enabled and you still have trouble viewing the applets, please let Bill Casselman know about it.
1. The three-body problem
There are several classic and well known periodic solutions to the three body problem of Newtonian mechanics:
| 1. Three bodies rotating around in a relatively simple circular motion - the Lagrangian systems. The Trojan asteroids, forming triplets along with Jupiter and the Sun, essentially move according to this scheme. These systems are not always stable. |  |
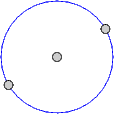 | 2. Three bodies rotating, but so as to remain constantly in a line. This was apparently first discovered by Euler. Such a system is always unstable, and cannot be expected to be found in reality. |
| 3. Some systems discovered by G. W. Hill (1838-1914), mimicking closely the Earth-Moon-Sun configuration, where two bodies move closely around each other while both of them together move around a third body far away. This work was in fact the origin of the differential equation now called Hill's equation. |
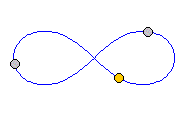
Recently a fourth solution has been found, of an entirely new type, in which three bodies of equal mass follow each other at a uniform spacing around an orbit in the shape of a figure eight. (Such solutions are called now choreographies because of the sometimes remarkable resemblance of the motion of the bodies to a group of ballet dancers.) This solution was first hinted at in a paper of Richard Moeckel in 1988, and then discovered empirically through computer calculations of Cristopher Moore in 1993. Very recently, it has been proven rigorously to exist by Alain Chenciner and Richard Montgomery, and explored in more detail through computer calculations of Carles Simó.
Periodic gravitational systems have been of great appeal for over two thousand years. Phenomena suggested by the results of Kolmogorov, Arnold, and Moser on periodicity have been explored extensively (if not thoroughly) by computation on simpler dynamical systems. But it seems that it wasn't until Moore's work in 1993 that computers helped to find new examples of periodic systems of astronomical interest. Of course just as with computer explorations of chaos, some people will be disturbed by the new problems raised by such purely experimental work. On the other hand, many of the numerical procedures so far used are extremely impressive, and deserve to be better known.
Moore and Joseph Gerver discovered empirically a few examples of similar orbits for N bodies with N larger than 3, but in some extraordinary computations Simó has gone on to find conjectural periodic orbits of the same type for many bodies. He hopes to expand this numerical work to a computer-assisted rigorous proof of the existence and properties of these orbits.
Simó has made some animations that can be run on UNIX systems with the program gnuplot, but here we have taken some of his data to make a few Java applets that do the same thing.
Welcome to the
Feature Column!
These web essays are designed for those who have already discovered the joys of mathematics as well as for those who may be uncomfortable with mathematics.
Read more . . .
Feature Column at a glance





