The Mathematics of Surveying: Part I
Posted May 2008.
Surveyors can work on a small scale (accurately siting the corners of a building on its plot) or a very large one (charting the path of a proposed highway) but their work always involves measurements in the field. ...
Tony Phillips
Stony Brook University
tony at math.sunysb.edu
Surveying and geometry
Tradition has it that geometry (literally, earth-measurement) began when the ancient Egyptians had to re-establish boundary lines between fields after the annual floods of the Nile; the United Nations Food and Agriculture Organization still recommends using a (3, 4, 5) triangle to set out right angles in survey work, a procedure that may well go back to the pharaohs. Today, surveyors continue to make explicit use of plane geometry and trigonometry on a day-to-day basis. Along with their seafaring cousins, the navigators, they may be the most geometrical of all professions. My plan in this column is to sample some of the more elementary current surveying procedures from a mathematical point of view, using The Surveying Handbook (edited by Russel Brinker and Roy Minnick, Van Nostrand Reinhold, New York, 1987) as my source.
It must be noted that at least one mathematician was a world-class surveyor. Laplace had advised the Académie des Sciences in 1791 on a new survey of the Paris meridian from Dunkerque to Barcelona (in order to establish the exact size of the earth and hence the length of the meter; the French Revolution had washed away, along with the traditional divisions of land, the units that had measured them). But Gauss himself conducted a survey of the state of Hanover between 1821 and 1825, and continued to direct work on refinements of the grid. One of the nine volumes of his collected works is entirely devoted to geodesy.
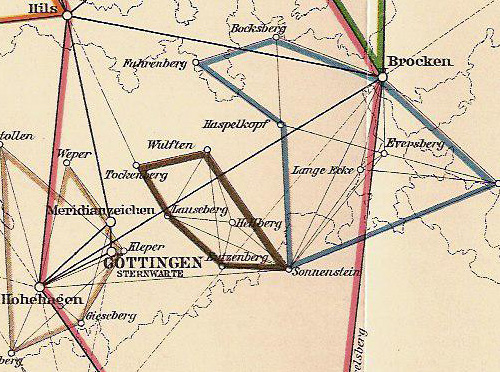
A detail of the triangulation of Hanover carried out under Gauss's supervision between 1820 and 1850. The pink lines are part of the Hauptsystem (main system) laid out by Gauss himself in 1821-1825. Collected Works, Volume 9, p. 347.
What is surveying?
According to the American Society of Civil Engineers, surveying is (in part) "The science and art of making all essential measurements in space to determine the relative positions of points and/or physical and cultural details above, on or beneath the earth's surface and to depict them in usable form." The words "in space" are significant: surveying is an outdoor activity. Surveyors can work on a small scale (accurately siting the corners of a building on its plot) or a very large one (charting the path of a proposed highway) but their work always involves measurements in the field.
Some theorems in plane geometry
One essential surveying task is "to prolong a straight line forward from an existing point." This is part of marking out on the terrain what will be a straight line on the map. If all points are visible from the starting point, line of sight may be used. But suppose a line has been drawn from point A to point B (in sight), and must be extended beyond B to a point visible from B but out of sight of A. Here is the procedure: move the transit (the surveyor's telescope) to B, backsight on A, "plunge" the transit (rotate it forwards in a vertical plane) and sight a new point C. This procedure requires two surveyors, one to look through the telescope and one to move a marker until it lines up with the telescope's axis; once executed it can be repeated to extend a line over hill and dale.
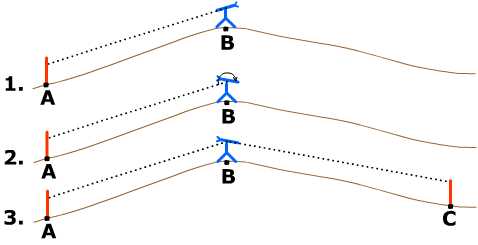 |
| Extending a line over irregular terrain. To extend the line AB to a point out of sight of A: 1. Transit is positioned at B and back-sighted at A. 2. Transit is "plunged" (rotated in vertical plane) to point forwards in terrain. 3. Point C is established in new transit line of sight. |
|
- The plunging, although described in the Handbook only as "more accurate" than turning 180o horizontally is in fact fundamental, since a straight line on the earth's surface is the intersection of that surface with a vertical plane (i.e. a plane passing through the center of the earth), in other words a segment of a great circle.
|
When the line needs extending through an obstruction, some more geometry comes into play. From the Handbook: "The transit is set up at B and deflection angle α, no larger than needed to clear the obstruction, is turned to locate C. Point C is occupied and an angle 2α is turned in the opposite direction from the first angle. D is established on the resulting prolongation of AB at the same distance as BC. Occupying D and turning a deflection angle α in the same direction as angle B produces line ABD ahead to E."
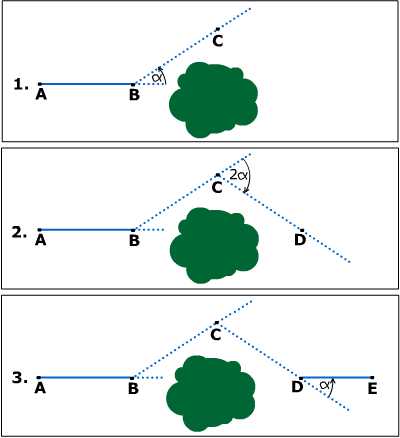 |
| To extend line AB beyond an obstruction: 1. Find appropriate point C at angle α from AB direction. 2. Turn angle -2α at C and locate point D such that CD = BC. 3. Turn angle α at D to locate E and extension of original line. |
|
- The collinearity of A, B, D and E follows from two theorems in plane geometry. The first (equivalent in fact to the parallel postulate) states that in a triangle each exterior angle is equal to the sum of the other two interior angles. The line AB extended through B must meet CD (since they make different angles with BC, they are not parallel), say at some point D'. The theorem guarantees that triangle BCD' has equal base angles; therefore, by a second theorem, the two opposite sides are also equal, so CD' = BC = CD and D' = D, so A, B, D are collinear. The mirror-image argument shows that B, D, E are collinear, and so all four points are. The Handbook goes on to say that distance BD may be calculated as 2 BC cos α.
|
Lengths and angles
A typical survey results in a map (also called "a survey"): a 2-dimensional representation of part of the earth's surface. A map being flat shows all points on the same level; but the surface of the earth is rarely flat. I am not referring here to the curvature of the earth --which large-scale surveys must take into account-- but to the local ups and downs that every cyclist is aware of. One of the jobs of the surveyor is to convert measurements taken on the undulating actual surface of the planet into data that represent positions on the ideal, perfectly level plane of the survey. As the Handbook remarks, "Considerable practice is required for field personnel to do accurate taping in hilly or rolling terrain."
This is the first place where trigonometry is mentioned in the Handbook. "In reducing slope measurements to their horizontal lengths, ..., a correction must be applied to the measured distance equal to the difference between the hypotenuse l and side d of a right triangle having its vertical side h." Sometimes the height difference h between two points can be measured directly. In that case the correction is given as Ch = h2/2l + h4/8l3. At other times the only possible measurement is the inclination from the horizontal of the line between the points; in terms of this angle α (the "vertical angle") the correction is Ch = l(1 - cos α).
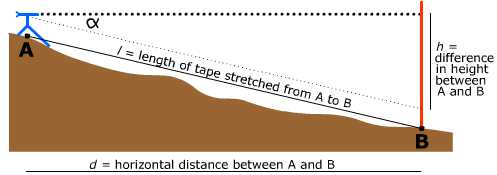 |
| Correction for slope: the tape measurement l of the distance from A to B is corrected to give the horizontal distance d between them by subtracting a correction term Ch given either in terms of the height difference h between the two points or in terms of the angle α between the tape and the horizontal. |
|
|
Trigonometry also enters into the measurement of distances when the operation is carried out optically, using stadia lines.
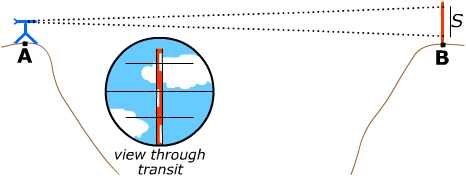
This procedure is called stadia tacheometry (or tachymetry), referring to the speed with which it can be carried out. To measure the distance from point A to point B, the surveyor at A focuses a telescope equipped with stadia lines on a graduated vertical rule held by the surveyor at B. The stadia lines are two short horizontal lines drawn above and below a central horizontal line in the focal plane of the telescope; these lines appear superimposed on the image and intersect a length S ("the stadia intercept") on the rule held at B, which can be read off by the observer. The distance between the stadia lines is such that if the observation is made horizontally, the distance D between A and B is 100 times the stadia intercept: D = 100 S.
|
|
- Similar triangles give the geometrical basis for this procedure: the stadia lines are mounted in the telescope so that the distance s between them is 1/100 of their distance d to the eyepiece.
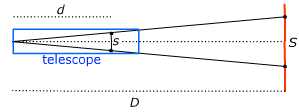
The similar triangles in the diagram yield that the ratio D/S between the distance D to the measuring rod and the observed stadia distance S must equal the ratio d/s = 100. Hence D = 100S.
|
Now suppose stadia tacheometry is carried out on a slope. The angle α of the slope between points A and B will affect the stadia intercept.

In the slanted perspective, points on the rule seem closer to each other than they are, so the apparent stadia intercept is too large; multiplying it by a factor of cos α has the same effect as turning the rule to be perpendicular to the line of sight, and corrects the distortion due to the angle. The straight-line distance from A to B is then D =100 S cos α. The horizontal distance from A to B will require an additional factor of cos α , as above, while the vertical distance is given by h = 100 S cos α sin α = 100 S (1/2) sin 2α, as recorded in the Handbook.
Areas
From the Handbook: "Land is ordinarily bought and sold on a basis of cost per unit area. For this reason as well as many others, an accurate determination of tract area is often necessary." The surveyor measures angles and distances. Once a "closed traverse" has been accomplished, i.e. a series of line segments that comes back to its initial point, the enclosed area (the "traverse area") may be computed. The Handbook explains three methods: the DMD method (for Double Meridian Distance), the coordinate method (both of these require a rectangular coordinate system), and the measurement of area by planimeter.
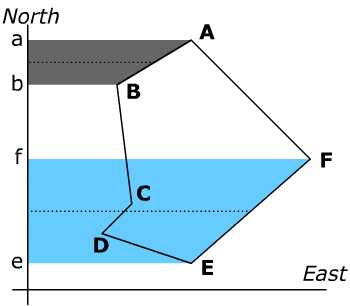
The DMD method. First some terminology: The latitude of a line segment is "its orthographic projection onto the north-south axis of the survey. North latitudes are considered positive, south latitudes negative" its departure makes analogous use of the east-west axis. In the DMD method we associate to each segment of the traverse its meridian distance: the perpendicular distance from its midpoint to the north-south axis. The DMD method calculates the traverse area by mutliplying the latitude and meridian distance of each line in the traverse, summing those products, and taking the absolute value of the sum. (The Handbook uses the double meridian distance, somewhat handier to calculate from the departures of consecutive lines, and then divides by 2 at the end; hence the name DMD).
|
|
- The latitude of line AB is minus the length of ab, since the line runs south. Hence the product of its latitude and its meridian distance is minus the area of the trapezoid ABba. On the other hand line EF runs north, so its latitude is (plus) the length of ef, and the product: latitude times meridian distance is equal to the area of the trapezoid EFfe. When the trapezoid areas are added with their signs, the total gives exactly the area enclosed by the traverse. If the computation had proceded clockwise (e.g. AFEDCBA), or if the traverse had been west of the north-south axis of the survey, the total would have given minus the area. The absolute value built into the procedure takes care of that minus sign.
|
The coordinate method. This method uses (x,y) coordinates for all the corners in the traverse. The procedure is "to multiply the x-coordinate of each corner by the difference between adjacent y-coordinates, add the resulting products, and take half the absolute value of the sum." The Handbook gives the formula:
A = [x1(y2 - yn) + x2(y3 - y1) + ... + xn(y1 - yn-1)]/2.
The planimeter method. This method will be discussed more in detail in next month's column. Here let me remark that the underlying mathematics is directly related to the coordinate method. Suppose we want to evaluate the area enclosed by a traverse given parametrically as x = f (t), y = g(t), for t running from a to b, with f(a) = f(b) and g(a) = g(b). We can approximate the curve with an n-segment polygonal line by taking Δt = (b - a)/n, setting t0 = a , t1 = a + Δt, t2 = a + 2 Δt, ... tn = a +n Δt = b, and considering the traverse with corners at (f(ti), g(ti)), i = 1 ... n (note that 0 and n give the same corner) and with enclosed area An. The Handbook's formula for the polygonal area gives (distributing the 1/2)
An = [f(t1)[g(t2) - g(tn)]/2 + [f(t2)[g(t3) - g(t1)]/2 + ... + [f(tn)[g(t1) - g(tn-1)]/2.
In the i-th term, the factor [g(ti+1) - g(ti-1)]/2 can be written, as a first order approximation, as [g'(ti) (2 Δt)]/2, giving An approximately as f(t1)g'(t1) Δt + ... + f(tn)g'(tn) Δt. In the limit as n goes to infinity these sums converge to the integral 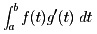 which planimeters are designed to compute.
which planimeters are designed to compute.
Volumes
Often in construction projects large quantities of material must be excavated at one place (a "borrow pit") to be filled in at another. The Handbook gives a procedure for estimating the amount of material that has been removed: The surveyors set up a horizontal grid over the area to be excavated (grid lines lines are typically 30 or 40 feet apart). Height measurements in feet are made at all the grid points before and after the excavation. The points are labelled 1, 2, 3 or 4 according to the number of grid rectangles they abut, and the volume estimate is given schematically by the formula
V = (A/4) (Σ h1 + 2Σ h2 + 3Σ h3 + 4Σ h4)
where A is the area of a grid rectangle, and Σ h1 represents the sum of all the height differences coming from grid points abutting only 1 square, Σ h2 is the sum coming from points abutting 2 squares, etc. The Handbook's formula has an extra 27 in the denominator to give a result in cubic yards.
|
|
- The volume over the grid is estimated as a sum of "prisms" obtained by linear interpolation between the four heights given at the corners of each grid square.
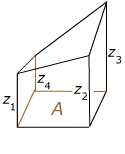 The use of these prisms is a 3-dimensional analogue of the trapezoid rule for estimating integrals of functions of one variable. Each one has volume V = A(z1 + z2 + z3 + z4)/4 , where A is the area of the base and z1, z2, z3, z4 are the heights at the four corners. When the volumes of all the prisms are summed up, each corner height zi will occur once for each prism that its edge abuts, so 1, 2, 3, or 4 times according to the position of its base point in the grid, leading to the formula in the Handbook . The use of these prisms is a 3-dimensional analogue of the trapezoid rule for estimating integrals of functions of one variable. Each one has volume V = A(z1 + z2 + z3 + z4)/4 , where A is the area of the base and z1, z2, z3, z4 are the heights at the four corners. When the volumes of all the prisms are summed up, each corner height zi will occur once for each prism that its edge abuts, so 1, 2, 3, or 4 times according to the position of its base point in the grid, leading to the formula in the Handbook .
|
Next month, Bill Casselman will have Part II of the mathematics of surveying.
Tony Phillips
Stony Brook University
tony at math.sunysb.edu












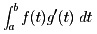 which planimeters are designed to compute.
which planimeters are designed to compute.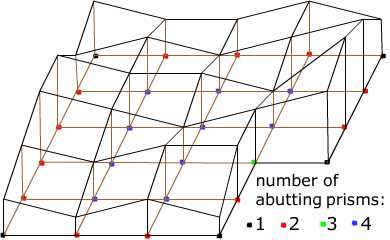
 The use of these prisms is a 3-dimensional analogue of the trapezoid rule for estimating integrals of functions of one variable. Each one has volume V = A(z1 + z2 + z3 + z4)/4 , where A is the area of the base and z1, z2, z3, z4 are the heights at the four corners. When the volumes of all the prisms are summed up, each corner height zi will occur once for each prism that its edge abuts, so 1, 2, 3, or 4 times according to the position of its base point in the grid, leading to the formula in the Handbook .
The use of these prisms is a 3-dimensional analogue of the trapezoid rule for estimating integrals of functions of one variable. Each one has volume V = A(z1 + z2 + z3 + z4)/4 , where A is the area of the base and z1, z2, z3, z4 are the heights at the four corners. When the volumes of all the prisms are summed up, each corner height zi will occur once for each prism that its edge abuts, so 1, 2, 3, or 4 times according to the position of its base point in the grid, leading to the formula in the Handbook .