
Mathematical ImageryMathematical artists create strong, stunning works in all media and explore the visualization of mathematics
ICERM Illustrating Mathematics
ICERM's Illustrating Mathematics Semester, held in fall 2019, brought together mathematicians, makers, and artists who share a common interest in illustrating mathematical ideas via computational tools. The program introduced mathematicians to new computational illustration tools to guide and inform their research; sparked collaborations among and between mathematicians, makers and artists; and found ways to communicate research mathematics to as wide an audience as possible. Here are images of works exhibited during the Illustrating Mathematics Semester.

Digital print, 60 x 90 cm, 2018. The inspiration for these visualizations came from attending a talk by Persi Diaconis in 2017. I wanted to know if I could better understand the mathematics of card shuffling by aesthetically exploring the various permutations underlying the shuffling methods. My motivation was to make these invisible structures visible and create elegant and interesting art in the process. These are visualizations of eight different ways of shuffling sixty-four cards. The horizontal lines of dots represent the particular orders of the cards throughout each shuffle, and the vertical curves represent the paths the cards take from start to finish. The cards are restored to the original order in all the eight cases. From left to right, top to bottom, the shuffles are: (1) Six perfect out-shuffles with two piles. (2) Three perfect in-shuffles with sixteen piles. (3) Four sixteen-card cuts from the top. (4) Seven milk shuffles. (5) Four "count-out-and-transfer" shuffles. (6) Twelve perfect in-shuffles with two piles. (7) Six alternating in- and out-shuffles with sixteen piles. (8) Twelve "deal-one-and-skip-one" shuffles. See details of card shuffling variations. --- Roger Antonsen

Digital art, 10 x 8 cm, 2019. In numerical cellular decomposition, a computer program repeatedly solves an ODE. Decomposition of the sphere takes a total of 78 paths. Most of them are entirely over the complex numbers, with few ending at real points on the sphere itself. Here we see those few paths, with their jaggedness coming from numerical predicting and correcting as the homotopy paths are walked. Consider the tremendous amount of computation that happens in our daily lives: how much of it is hidden from us, the focus on result and outcome, and the bliss of ignorance to process. Such are the paths to this sphere. --- Danielle Amethyst Brake
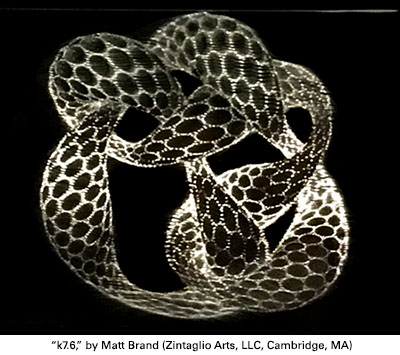
Specular hologram (micro-engraved sheet metal), 28 x 36 cm, 2013. This is a metal plate that reflectively produces 3D imagery of a snake-skinned k7.6 knot. When lit by a small light source, the surface microtexture reflects thousands of glints of light, which appear to travel across the plate when motion of the eye, plate, or light changes the optical path. For certain motions, the 2D travel can be made consistent with the projection of a rigidly moving 3D point cloud. Adding occlusion effects then leads the brain to interpret the glints as a solid 3D scene. The inspiration for developing this technique: a curious glint on a piece of curved tinsel spied in the Artesia Lounge, a beloved 80's blues/dive bar. See a collection of animated knots. --- Matt Brand

Specular hologram (micro-engraved sheet metal), 28 x 36 cm, 2013. This is a metal plate that reflectively produces 3D imagery of a toric knot. Zintaglio Arts develops new and unexpected visual experiences for museums, public venues, and arts festivals. We aim to please the eye and pique the curiosity. Leveraging under-appreciated perceptual and optical phenomena, we develop novel optimization and fabrication techniques that endow prosaic materials with new optical properties, turning them into imaging devices. Recent installations have featured holographic sheet metal, photographic shower glass, videographic sunshades, and pictographic chain-link fences. See more knots.--- Matt Brand

3D print, orange nylon, 20 x 20 x 10 cm, 2012. My artistic passions are purely mathematical images and sculptures, which express a certain vision of forms and shapes: my interpretations of distance, transformations, and space. This is a limit set of a group generated by inversions in eight spheres centered at the vertices of a cube as well as a chain of four symmetrically placed intersecting spheres surrounding that cube. The limit set is intricate composition of simpler limit sets of a pair of subgroups. These are given by two subsets of generators: the eight cube-based generators and then the chain of four spheres. --- Vladimir Bulatov
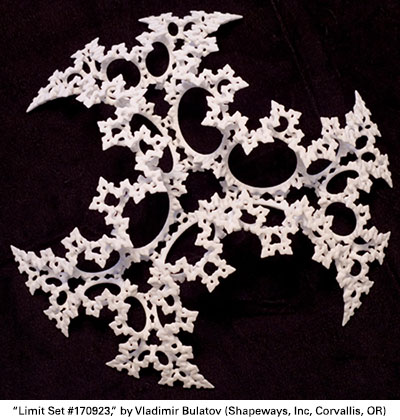
3D print, white nylon, 20 x 20 x 10 cm, 2017. Escher's "Circle Limit" woodcuts are based on symmetry groups generated by inversions in three circles. The limit sets of these groups are always contained in a round circle. Group generated by inversions in spheres can be much more complicated. Such a group, with only four generators, has a perhaps highly intricate limit set contained in a round sphere. However, as shown here, five or more generators can produce limit sets with truly three-dimensional structure. To calculate these limit sets we used a "reverse mapping", taking each point in space into a fundamental domain for the group. We use the inverse Jacobian to measure the distance to the limit set. --- Vladimir Bulatov

3D print, black nylon, 20 x 20 x 20 cm, 2017. My images and sculptures are like photographs of interesting mathematical ideas, which I discover and bring to the real world. I have always been intrigued by the possibility of showing the intrinsic richness of the mathematical world, whose charm and harmony can be appreciated by everyone. This is a limit set of a group generated by inversions in two orthogonal planes and three spheres arranged inside of the wedge formed by the planes. --- Vladimir Bulatov

3D print, red nylon, 20 x 20 x 20 cm, 2014. This work is a limit set of a group generated by inversions in eight spheres centered at the vertices of two concentric tetrahedra of different size. The limit set is a intricate composition of a simpler spherical limit sets of a pair of subgroups. Each subgroup is generated by inversions in four spheres centered on the vertices of one tetrahedron. This creates an interplay of structures with tetrahedral symmetry. --- Vladimir Bulatov

Digital print, 90 x 70 cm, 2019. This is an illustration of the two-twist spun trefoil that was inspired by the works of Satoh and Shima, Inoue, and Kawamura. I used techniques developed by Saito and myself to create the image: movie moves and surface charts. A perspective change occurs in the middle level at which front and back are reversed. --- Scott Carter

Digital print, 100 x 72 cm, 2019. This is the connected sum of an unknotted projective plane and a twist spun trefoil as a subset of four-dimensional space. It is knotted since it is three-colorable. --- Scott Carter
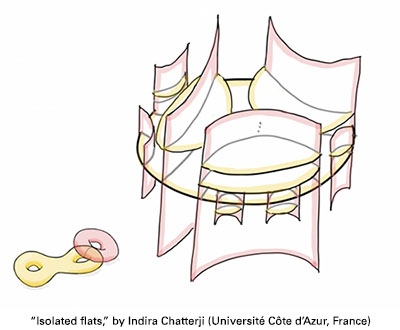
Gif (still), 2018. Indira Chatterji is a geometric group theorist, presently working at Université de Nice in France. She started illustrating groups in an attempt to make general audience talks on geometric group theory more enticing to a wider audience. Here is the universal cover of a genus two surface glued to a torus along a simple closed geodesic, an example of a CAT(0) space with isolated flats. See the animated gif. --- Indira Chatterji

Photographic print of high-res map generated with Mathematica, 40 x 56 cm, 2019. "The Beauty of Roots" unveils the hierarchical algebraic structure of the connectivity locus M for a family of self-similar sets studied over the past 35 years. Some mathematicians who studied M include Michael Barnsley, Thierry Bousch, Christoph Bandt, Boris Solomyak, John Baez, Bill Thurston, Danny Calegari, Sarah Koch, Alden Walker, Pablo Shmerkin, Stefano Silvestri, and the author himself Bernat Espigule. This diagram shows all roots of polynomials up to degree 12 with coefficients 1, -1, and 0, always starting with 1. The radius and color-coding of each algebraic number comes from the degree m of the lowest degree polynomial who has it as a root. This original picture came to the author after proving a theorem related to complex trees. --- Bernat Espigulé

3D printed with ABS plastic, designed in Mathematica, 10 x 100 x 50 cm, 2019. Complex trees are two-dimensional objects living in the complex plane, but they can be represented in 3D by adding a certain depth at each branching level. The specimens selected for this mathematical arboretum are complex trees with a plane-filling tipset that can be used to tile the entire plane. From left to right trees in the bottom are $T\{-0.3376 + i 0.5623, -0.1226 - i 0.7449\}$, the tame twin dragon tree $T\{(1+i\sqrt{7})/4,-(1+i\sqrt{7})/4\}$, and the twin dragon tree $T\{1/2+i/2,-1/2-i/2\}$. In the front row we have a pair of ternary complex trees with a Rauzy fractal tipset on the left, and the fludgeflake tree $T\{i\sqrt{3},1/2-i/(2\sqrt{3}),-1/2+i/(2\sqrt{3})\}$ on the right. --- Bernat Espigulé

Digital media animation, 36 x 64 cm, 2019. See the animation video, which explores the parameter space of a newly discovered family of tipset connected ternary complex trees related to the Sierpinski triangle. The parameter space for this family is defined in the annulus $\{z=x+iy : 1/4 < |z| < 1\}$. Starting at $t=0$ and ending in $t=2\pi$, each frame $M_c(t)$ shows in black the parameters $z$ that generate ternary complex trees $T\{z,1/2,1/(4z)\}$ with at least a tip point landing in $c(t):=1+\exp((i t)/2)$. The fast algorithm to generate $M_c(t)$ that made this animation possible was recently discovered by the author. Because of the asymptotic similarity between $M_c(t)$ and self-similar sets $F\{z,1/2,1/(4z)\}$ with parameter $z$ in $M_c(t)$, this animation is a novel way to illustrate what is out there in the blink of an eye. --- Bernat Espigulé

Digital print on aluminum, 51 x 51 cm, 2019 I created a wallpaper pattern using a suitable wallpaper function, the domain-coloring algorithm, and a photograph of sweet peas. Then I wound the wallpaper around the plane in a Fibonacci spiral. The morphing effect is produced by the simple artifice of turning the coloring photograph as the computation proceeds along the spiral arms: It's as if the pattern is gradually turning from white to purple as we progress outward. (This effect can also be shown in animation, thanks to the "blooming" property of Fibonacci spirals, as pioneered by John Edmark, whose work inspired this piece.) The title comes from a curious sentence in an Italian lesson on Duolingo, the free language-learning app. --- Frank A. Farris

Laser etched glass, 10 x 10 x 10 cm, 2005. I design for 3D printing in steel and laser etching in glass. In metal, I'm a sculptor using hand and algorithmic techniques, most recently in collaboration with a large generative engine which I'm writing in Rhinoceros/Grasshopper/Python. In glass, I work as a scientific illustrator rendering observed and modeled 3D data, both on commission and as a lifelong fan of all science. A Calabi-Yau manifold, projected into 3-space by Dr. Andrew J. Hanson of Indiana University. --- Bathsheba Grossman

Steel/bronze, glass, 11 x 11 x 11 cm, 2016. A hand designed 3D printed puzzle, rendered in sintered steel/bronze composite metal by Ex One and embellished with fused glass and magnetic closures. --- Bathsheba Grossman

Steel/bronze, 10 x 10 x 10 cm, 2005. A mathematically generated 3D print, rendered in sintered steel/bronze composite metal by Ex One. --- Bathsheba Grossman

Video (still), 2012. This short video shows the embedding of an (abstract) flat torus in 3D ambient space. The fractal aspect of the embedding results from the Convex Integration process, which accumulates corrugations on a given initial non-isometric torus. See more information on the Hevea project site.
It follows from a simple curvature obstruction that a flat torus cannot be isometrically embedded in Euclidean 3-space. From the same obstruction, neither can a sphere be isometrically reduced to fit in the interior of a ball of smaller radius. However, sixty years ago, John Nash and Nicolas Kuiper demonstrated the existence of such isometric embedding or reduction if we just require the isometric maps to be C1. Misha Gromov later developed the Convex Integration theory as a powerful tool to construct such maps. Nonetheless, until a few years ago no one had been able to visualize those paradoxical surfaces. Here, we present images and 3D printings of the Hevea Project computed thanks to the convex integration theory of Gromov.--- Vincent Borrelli, Roland Denis, Francis Lazarus, Boris Thibert and Damien Rohmer

Plastic powder for 3D printing, 25 x 25 x 25 cm, 2015. This 3D printing displays an isometrically reduced sphere. See more information on the Hevea project site. --- Vincent Borrelli, Roland Denis, Francis Lazarus, Boris Thibert and Damien Rohmer

Digital print on metal, 20 x 25 cm, 2007. I created this image of a variant of the Alexander horned sphere while taking a course called "the Art and Science of Computer Graphics," taught by Duane Bailey, as an undergraduate at Williams College. The 3D set depicted here in gold is homotopic to a solid ball in 3-space; one might imagine continuously retracting the "arms" of the object and watching it shrink down to become a round ball. The complement of this set in Euclidean 3-space, however, has a much more complicated topological structure than the complement of a geometrically round ball. --- Kathryn Lindsey
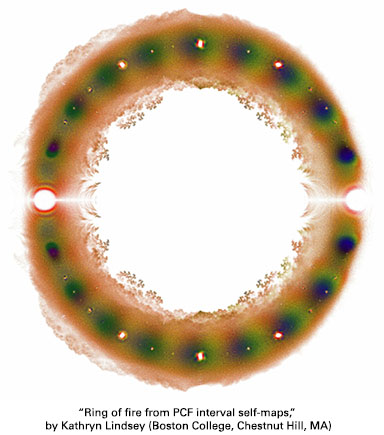
Digital print on canvas, 76 x 76 cm, 2017. Joint with Harrison Bray, Diana Davis, and Chenxi Wu. This plot was created using Mathematica at an AMS Mathematics Research Community program on "Dynamical Systems: Smooth, Symbolic & Measurable" as part of our joint research on the growth rates of post-critically finite interval self-maps. It is a plot of all Galois conjugates of growth rates of post-critically periodic generalized beta transformations with a growth rate in [1,2] and critical period at most 22, colored according to the critical period. The project culminated in our research paper, "The Shape of Thurston's Master Teapot" (2019, preprint on ArXiv.org). --- Kathryn Lindsey

Black and white, 55,653 circles on heavy matte paper, 152 x 91 cm, 2019. From an exhibit of 9 prints at Harvard University, illustrating totally geodesic surfaces in hyperbolic 3-manifolds. --- Curtis McMullen

Mirrors attached to plastic tiles, 30 x 30 x 30 cm, 2019. Looking into the two Archimedean solids provides a view into a hypnotic mirror world that is reminiscent of the view into hyperbolic three manifolds. --- Yana Mohanty and Bjoern Muetzel

Photograph, 30 x 30 cm, 2019. When you attach mirror surfaces to the faces of a rhombicosidodecahedron, and you look inside, the result is mesmerizing. We wanted to explore the experience through the eye of a spherical camera placed near the center of the solid. The final image is approximately the stereographic projection from the "pole" through which the camera is placed. Careful placement of the camera allows us to see reflections of pentagons in other pentagons and squares. See more details. --- Yana Mohanty and Bjoern Muetzel

Photograph, 30 x 30 cm, 2019. What happens when you attach mirror surfaces to the inside faces of a rhombicosidodecahedron? We set out to find this out by placing a spherical camera near the center of the solid and then stereographically projecting the output. In this image, the "pole" of the projection was the face opposite to the one through which the camera was placed. Each “petal” of the flower is the image of a decagon (formed by the boundary of a pentagon surrounded by triangles and squares) on the actual rhombicosidodecahedron, taken to almost circles by the stereographic projection. Careful placement of the camera allows us to see reflections of pentagons in other pentagons and squares. See more details. --- Yana Mohanty and Bjoern Muetzel

Porcelain, reduction glazes, 35 x 35 x 3 cm, 2018. This is a porcelain tray slip-cast in the Muira paper folding pattern. The glazing is done in cone 10 reduction glazes. To create this tray, I folded the form in paper, then cast the paper form into kiln-slumped glass, and then cast the resultant glass surface into a plaster mold for a final slip-casting in porcelain. The tray can be used, displayed on a tabletop, or wall-mounted. --- Caleb Nussear

Gouache on gampi, 42 x 53 cm, 2003. This painting, "udo 31" is an open net of repeating marks and random breaks hung on a triangular grid. The three sizes of marks are put down in four layers. The layer with lightest color value is sandwiched between the darker top and bottom layers, creating an ambiguous space. The disruptions of the pattern facilitate movement throughout the painting. --- Jacqueline Ott

3D printed nylon plastic, 7 x 15 x 15 cm, 2015 The figure-eight knot, the most common knot after the trefoil, is widely used in sailing and rock-climbing. The sculpture here contains the complement of the figure-eight knot - the part of space outside of the knot. The core curve is parametrised in the three-sphere then stereographically projected to three-space. Let $A(t) = \varepsilon \sin 4t$. Then the parametrization is given by $w(t) = (1 - A(t)^2) (\lambda \sin t - (1 - \lambda) \sin 3t)/(1 + A(t)^2)$ $x(t) = (1 - A(t)^2) (\lambda \cos t + (1 - \lambda) \cos 3t)/(1 + A(t)^2)$ $y(t) = (1 - A(t)^2) (2\sqrt{\lambda - \lambda^2} \sin 2t)/(1 + A(t)^2)$ $z(t) = 2 A(t)/(1 + A(t)^2)$ We chose the values $(0.25,0.16)$ for the parameters $(\lambda, \varepsilon)$. --- François Guéritaud, Saul Schleimer, and Henry Segerman

3D-print, ABS plastic, 19 x 19 x 19 cm, 2019. This sculpture was inspired by Charles O. Perry's 18-inch sand-cast sculpture called "Star Cinder," which is based on the icosahedral tangle of ten equatorial triangular loops. For my own sculpture, each original (3,1)-torus-knot loop has been replaced with a (3,3)-torus-knot, which corresponds to three mutually interlinked circles. Thus the whole configuration consists of a tangle of 30 circles--one each for every edge of an icosahedron. The challenge was to construct a single 2-manifold "soap-film" surface between those 30 border curves that retains the full symmetry of the oriented octahedron. The presented solution has three concentric, radially coupled shells, each with 20 triangular and 12 pentagonal openings. --- Carlo Séquin

13 x 70 x 13 cm, designed with MATLAB and OpenSCAD; 3D printed with SLA resin and supports, 2019. In collaboration with mathematician Steve Lucas, we recently developed a computationally reasonable method for creating 3D-printable models of chaotic attractors. This collection of five designs provide three-dimensional physical, tangible versions of the beautiful two-dimensional renders created by artist and photographer Phillipe Put. Our method takes as input a set of differential equations and initial values, produces a sequence of datapoints in MATLAB spaced by curvature constraints, and "sweeps" that data into a curve-surrounding polyhedron in OpenSCAD. The image shows our 3D printed model of the Aizawa Attractor. Four other models are currently in production and will be completed by August 2018. See more details. --- Laura Taalman / mathgrrl

10 x 14 x 13 cm, designed with KnotPlot, MeshLab, TopMod, and Meshmixer; 3D printed in full color with powder and binder jetting, 2017. This model illustrates a continuous morphing between the two knot conformations known as the Perko Pair. The red knot is "Perko A", the knot known as 10161 in the Rolfsen table. The purple knot is "Perko B", the Knot Formerly Known As 10162. The remaining knots are snapshots of a continuous morphing from Perko A to Perko B that shows that they are, in fact, the same knot. Each knot in the morph was extracted from KnotPlot, Laplacian thinned in Meshlab, Catmull-Clark remeshed in TopMod, and then arranged, scaled, and painted with color in Meshmixer. See more details. --- Laura Taalman / mathgrrl

19 x 21 x 20 cm, designed with KnotPlot, TopMod, and Cura; 3D printed with FDM in yellow Polylactic Acid and custom supports, 2018. This knot conformation is halfway between "Perko A" and "Perko B", the two knots in the Rolfsen knot table that were famously shown to be equivalent by Kenneth Perko in 1973. Extrusions were added to each mesh face in the model to create spikes that highlight the path of the knot through three-dimensional space. Designed with KnotPlot and TopMod, optimized for 3D printing with Cura. The spikes make the model extremely challenging to print on a desktop 3D printer. After many unsuccessful print attempts, the final model took over six days to print and an additional week to clean up breakaway support material and for post-processing. See more details. --- Laura Taalman / mathgrrl

5 x 50 x 5 cm, designed with OpenSCAD, Mathematica, Blender, and KnotPlot; 3D printed with Direct Metal Laser Sintering, 60% Stainless Steel / 40% Bronze, 2018. Knots are embeddings of circles in 3-dimensional space, but they are typically studied in terms of their projections into 2-dimensional space. We can use 3D printed models to investigate knots in a more 3-dimensional way. In this series, we present nine Stainless Steel 3D printed knot conformations: Tritangentless Trefoil, Figure Eight Stick Knot, Cinquefoil Lattice, 52 Lissajous, 62 Petal Knot, two (7,2) Torus Knots, 819 Hyperboloid Stick Knot, and a Midway Perko Knot. Knot conformations were chosen based on key properties of each knot from the literature. The knots were scaled before construction to form a consistent series while preserving thickness. Designed with OpenSCAD as well as Mathematica, Blender, and Knotplot. See a video with more details. --- Laura Taalman / mathgrrl

3d-printed bronzed steel, 8 x 8 x 8 cm, 2018. In my mathematical art, I seek to reify the abstract, to make mathematical concepts and shapes available to touch, to trace, to twist and turn. To create physical artifacts meant for interaction to bring the complex closer and make the abstract concrete. In this work three surfaces can be constructed by identifying opposite sides of a square. They are distinguished by twisting pairs of sides before gluing--like with a Möbius strip. By twisting both pairs of sides, we construct the Projective Plane. Like the Klein Bottle, the Projective Plane cannot be represented in 3-dimensional space without self-intersections. This particular shape, the Roman Surface, is a projection of an important construction from algebraic geometry: the Veronese Embedding. --- Mikael Vejdemo-Johansson



