
Mathematical ImageryMathematical artists create strong, stunning works in all media and explore the visualization of mathematics
Vizzie Winners
The National Science Foundation and Popular Science are cosponsors of the long-running Visualization Challenge, now called The Vizzies, to recognize some of the most beautiful visualizations from the worlds of science and engineering. "Some of science's most powerful statements are not made in words. From DaVinci's Vitruvian Man to Rosalind Franklin's X-rays, science visualization has a long and literally illustrious history. To illustrate is to enlighten! Illustrations provide the most immediate and influential connection between scientists and other citizens, and the best hope for nurturing popular interest. They are a necessity for public understanding of research developments."
— National Science Foundation

First Place, Illustration - 2006 Visualization "Vizzies" Challenge (National Science Foundation). Innumerable surfaces that we cannot touch or see or even know can be seen by mathematicians. They have long relied on their powers of imagination to picture abstract surfaces. Richard Palais of the University of California, Irvine, and graphic artist Luc Benard used the magic of computer graphics to recreate these abstract surfaces in familiar yet intriguing settings.
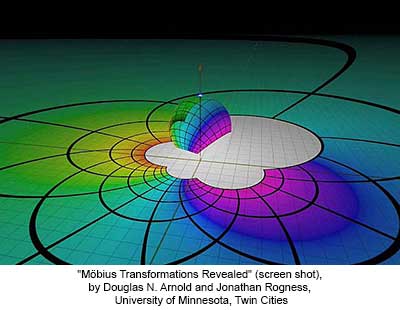
Honorable Mention, Noninteractive Multimedia (screen shots) - 2007 Visualization "Vizzies" Challenge (National Science Foundation). Any real numbers can be plotted on a line that runs from negative to positive infinity, but throw in an imaginary component and the line becomes a plane, where complex numbers are plotted on both the real and the imaginary axes. Möbius transformations are mathematical functions that send each point on such a plane to a corresponding point somewhere else on the plane, either by rotation, translation, inversion or dilation. It may sound confusing, but after watching this simple and elegant explanation of Möbius transformations created by Douglas N. Arnold and Jonathan Rogness of the UNM, everything becomes clear.

First Place, Illustration - 2009 Visualization "Vizzies" Challenge (National Science Foundation). Sketch a line and then draw a point off it. How many lines parallel to the first line can you draw through that point? The Greek mathematician Euclid said just one, but for more than 2,000 years after his death, mathematicians struggled to prove that he was right based on his other geometric rules. Then the 19th century Russian mathematician Nikolai Lobachevsky showed that you couldn't: In some circumstances, you can sketch an infinite number of lines through that point and not violate any of Euclid's other axioms. Mathematician Dick Palais of the University of California, Irvine, and digital artist Luc Benard wanted to convey the history of Lobachevsky's solution to this mathematical puzzle with their illustration.

Honorable Mention, Illustration - 2011 Visualization "Vizzies" Challenge (National Science Foundation). This illustration represents one example of a complex function. Such functions are mathematical relationships that incorporate both real and imaginary numbers, such as the square root of -1. To create this visualization, researchers at the Free University of Berlin assigned each complex number in their equation to a spot on a color wheel. The farther numbers get from zero, the brighter they are (white regions approach infinity). The result packs two dimensions of information (hue and brightness) into each point in the image.

Honorable Mention, Posters & Graphics - 2013 Visualization "Vizzies" Challenge (National Science Foundation). Soap bubbles are often perceived as majestic, but the physics of popping bubbles in a foam are far from simplistic. Delving into the multi-scale phenomena underpinning bubble dynamics, one finds that there is host of challenges that need to be solved if one is to model and simulate foam behavior with computers. This poster tells part of this story, from the picturesque behavior of soap bubbles, to multi-scale physics and mathematical modeling, to simulation with powerful supercomputers. See 2013 Vizzie Winners, including a link to a video of the foam simulation.
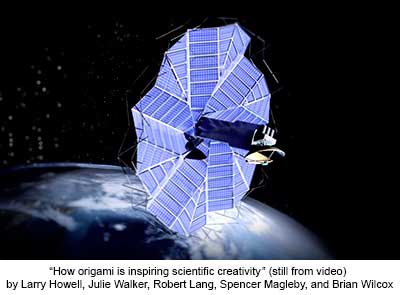
People's Choice for the video category, and People's Choice, Best Overall - 2015 Visualization "Vizzies" Challenge (National Science Foundation). Engineers use origami principles to design spacecraft solar panels and other devices that flex or unfurl, as in this video by a lab at Brigham Young University. Larry Howell, the team leader, says the work is just plain fun. "There's so much potential for applications. These things can really make a difference." View the video.


