Mathematical Concepts Illustrated by Hamid Naderi Yeganeh

This image shows 1,000 line segments. For each $i=1,2,3,\ldots\ldots,1000$ the endpoints of the $i$-th line segment are: $(-\sin(2\pi i/1000), -\cos(2\pi i/1000))$ and $((-1/2)\sin(8\pi i/1000), (-1/2)\cos(12\pi i/1000))$. I created this image by running my program on a Linux operating system.

This image shows 1,000 line segments. For each $i=1,2,3,\ldots,1000$ the endpoints of the $i$-th line segment are: $(-\sin(4\pi i/1000), -\cos(2\pi i/1000))$ and $((-1/2)\sin(8\pi i/1000), (-1/2)\cos(4\pi i/1000))$. I created this image by running my program on a Linux operating system.

This image shows 1,000 line segments. For each $i=1,2,3,\ldots,1000$ the endpoints of the line segment are: $(-\sin(8\pi i/1000), -\cos(2\pi i/1000))$ and $((-1/2)\sin(6\pi i/1000), (-1/2)\cos(2\pi i/1000))$. I created this image by running my program on a Linux operating system.

This image shows 1,000 line segments. For each $i=1,2,3,\ldots,1000$ the endpoints of the $i$-th line segment are: $(-\sin(10\pi i/1000), -\cos(2\pi i/1000))$ and $((-1/2)\sin(12\pi i/1000), (-1/2)\cos(2\pi i/1000))$. I created this image by running my program on a Linux operating system.

This image contains a heart-like figure. It shows 601 line segments. For each $i=1, 2, 3, \ldots. , 601$ the endpoints of the $i$-th line segment are:
$(\sin(10\pi (i+699)/2000), \cos(8\pi (i+699)/2000))$
and
$(\sin(12\pi (i+699)/2000), \cos(10\pi (i+699)/2000))$.

I created this image by running my program.

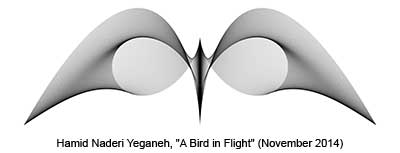
This image is like a bird in flight. It shows 2000 line segments. For each $i=1, 2, 3, \ldots , 2000$ the endpoints of the $i$-th line segment are:
$(3(\sin(2\pi i/2000)^3), -\cos(8\pi i/2000))$
and
$((3/2)(\sin(2\pi i/2000)^3), (-1/2)\cos(6\pi i/2000))$.

I created this image by running my program.

This image shows 10,000 circles. For each $i=1,2,3,\ldots,10{,}000$ the center of the $i$-th circle is:
$((\cos(38\pi i/10{,}000))^3, \sin(10\pi i/10{,}000))$ and the radius of the $i$-th circle is: $(1/3)(\sin(16\pi i/10{,}000))^2$.

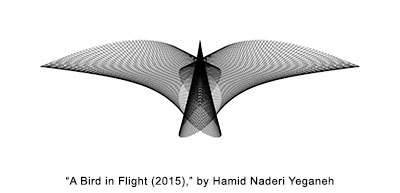
This image is like a bird in flight. It shows 500 line segments. For each $i=1,2,3,\ldots,500$ the endpoints of the $i$-th line segment are: $((3/2)(\sin((2\pi i/500)+(\pi /3)))^7, (1/4)(\cos(6\pi i/500))^2)$ and
$((1/5)\sin((6\pi i/500)+(\pi /5)), (-2/3)(\sin((2\pi i/500)-(\pi /3)))^2).$

This image is like a sailing boat. It shows 2,000 line segments. For each $k=1,2,3,\ldots,2000$ the endpoints of the $k$-th line segment are: $(\cos(6\pi k/2000)-i \cos(12\pi k/2000))e^{3\pi i/4}$ and $(\sin((4\pi k/2000)+(\pi /8))+i \sin((2\pi k/2000)+(\pi /3)))e^{3\pi i/4}.$

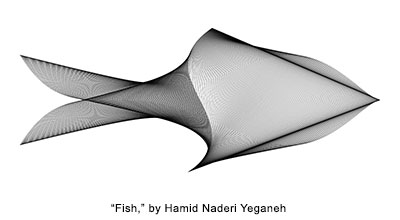
This image is like a fish. It shows 1,000 line segments. For $i=1,2,3,\ldots,1000$ the endpoints of the $i$-th line segment are: $(-2\cos(4\pi i/1000), (1/2)(\cos(6\pi i/1000))^3)$ and $(-(2/15)\sin(6\pi i/1000), (4/5)\sin(2\pi i/1000))$.

This image shows 4000 circles. For $k=1,2,3,\ldots,4000$ the center of the $k$-th circle is $(X(k), Y(k))$ and the radius of the $k$-th circle is $R(k)$, where

$\begin{array}{llll}X(k)&=&&(2k/4000)+(1/28)\sin(42\pi k/4000)\\&&+ &(1/9)((\sin(21\pi k/4000))^8)\\&&+ &(1/4)((\sin(21\pi k/4000))^6)*\\ && &\sin((2\pi /5)(k/4000)^{12}),\end{array}$

$\begin{array}{llll}Y(k)&=&&(1/4)(k/4000)^2\\&&+&(1/4)(((\sin(21\pi k/4000))^5) \\&& + &(1/28)\sin(42\pi k/4000))*\\&&&(\cos((\pi /2)(k/4000)^{12})),\end{array}$

$\begin{array}{lll}R(k)& =& (1/170)+(1/67)((\sin(42\pi k/4000))^2)*\\& &(1-((\cos(21\pi k/4000))^4)).\end{array}$

This image shows 40,000 circles. For $k=1,2,3,\ldots,40{,}000$ the center of the $k$-th circle is $(X(k), Y(k))$ and the radius of the $k$-th circle is $R(k)$, where

$\begin{array}{lll}X(k)&=&(6/5)((\cos(141\pi k/40{,}000))^9)(1-(1/2)(\sin(\pi k/40{,}000))^3)*\\&&(1-(1/4)((\cos(2\pi k/40{,}000))^{30})(1+(2/3)(\cos(30\pi k/40{,}000))^{20})-\\&&((\sin(2\pi k/40{,}000))^{10})((\sin(6\pi k/40{,}000))^{10})*\\&&((1/5)+(4/5)(\cos(24\pi k/40{,}000))^{20})),\end{array}$

$\begin{array}{lll}Y(k)&=&\cos(2\pi k/40{,}000)((\cos(141\pi k/40{,}000))^2)(1+(1/4)((\cos(\pi k/40{,}000))^{24})*\\&&((\cos(3\pi k/40{,}000))^{24})(\cos(19\pi k/40{,}000))^{24}),\end{array}$

$\begin{array}{lll}R(k)&=&(1/100)+(1/40)(((\cos(2820\pi k/40{,}000))^6)+\\&&(\sin(141\pi k/40{,}000))^2)(1-((\cos(\pi k/40{,}000))^{16})*\\&&((\cos(3\pi k/40{,}000))^{16})(\cos(12\pi k/40{,}000))^{16}).\end{array}$

This image shows 40,000 circles. For $k=1,2,3,\ldots,40{,}000$ the center of the $k$-th circle is $(X(k), Y(k))$ and the radius of the $k$-th circle is $R(k)$, where

$\begin{array}{lll}X(k)&=&(3/2)((\cos(141\pi k/40{,}000))^9)*\\&&(1-(1/2)\sin(\pi k/40{,}000))*\\&&(1-(1/4)((\cos(2\pi k/40{,}000))^{30})*\\&&(1+(\cos(32\pi k/40{,}000))^{20}))*\\&&(1-(1/2)((\sin(2\pi k/40{,}000))^{30})*\\&&((\sin(6\pi k/40{,}000))^{10})*\\&&((1/2)+(1/2)(\sin(18\pi k/40{,}000))^{20})),\end{array}$

$\begin{array}{lll}Y(k)&=&\cos(2\pi k/40{,}000)*\\&&((\cos(141\pi k/40{,}000))^2)*\\&&(1+(1/4)((\cos(\pi k/40{,}000))^{24})*\\&&((\cos(3\pi k/40{,}000))^{24})*\\&&(\cos(21\pi k/40{,}000))^{24}),\end{array}$

$\begin{array}{lllcl}R(k)&=&(1/100)&+&(1/40)(((\cos(141\pi k/40{,}000))^{14})+(\sin(141\pi k/40{,}000))^6)*\\&&&&(1-((\cos(\pi k/40{,}000))^{16})((\cos(3\pi k/40{,}000))^{16})*\\&&&&(\cos(12\pi k/40{,}000))^{16}).\end{array}$

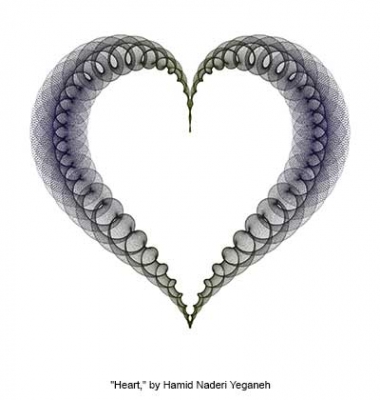
This image shows 2500 ellipses. For each $k=1,2,3,\ldots,2500$ the foci of the $k$-th ellipse are:
$A(k)+iB(k)+C(k)e^{68\pi i k/2500}$
and
$A(k)+iB(k)-C(k)e^{68\pi i k/2500}$
and the eccentricity of the $k$-th ellipse is $D(k)$, where
$A(k)=(-3/2)((\sin(2\pi k/2500))^3)+(3/10)((\sin(2\pi k/2500))^7),$

$B(k)=\sin((2\pi k/1875)+(\pi /6))+(1/4)(\sin((2\pi k/1875)+(\pi /6)))^3,$

$C(k)=(2/15)-(1/8)\cos(\pi k/625),$

$D(k)=(49/50)-(1/7)(\sin(4\pi k/2500))^4.$

This image shows 8,000 ellipses. For each $k=1,2,3,\ldots,8000$ the foci of the $k$-th ellipse are:
$A(k)+iB(k)+C(k)e^{300\pi ik/8000}$
and
$A(k)+iB(k)-C(k)e^{300\pi ik/8000}$
and the eccentricity of the $k$-th ellipse is $D(k)$, where
$\begin{array}{llll}A(k)&=&&(3/4)\sin(2\pi k/8000)\cos(6\pi k/8000)\\&&+&(1/4)\sin(28\pi k/8000),\end{array}$

$\begin{array}{llll}B(k)&=&&(3/4)\cos(2\pi k/8000)\cos(8\pi k/8000)\\&&+&(1/4)\cos(28\pi k/8000),\end{array}$

$\begin{array}{lll}C(k)&=&(1/18)+(1/20)\cos(24\pi k/8000),\end{array}$

$ \begin{array}{lll} D(k)&=&(49/50)-(1/7)(\sin(10\pi k/8000))^4.\end{array}$

This image shows 5600 ellipses. For each $k=1,2,3,\ldots,5600$ the foci of the $k$-th ellipse are:
$A(k)+iB(k)+C(k)e^{44\pi ik/5600}$
and
$A(k)+iB(k)-C(k)e^{44\pi ik/5600}$
and the eccentricity of the $k$-th ellipse is $D(k)$, where
$\begin{array}{lll}A(k)&=&(\cos(28\pi k/5600))^3,\end{array}$


$\begin{array}{llll}B(k)&=&&\sin(28\pi k/5600)\\&&+&(1/4)(\cos((14\pi k/5600)-(7\pi /4)))^{18},\end{array}$


$\begin{array}{lll}C(k)&=&(1/70)+(1/6)+(1/6)\sin(28\pi k/5600),\end{array}$


$\begin{array}{lll}D(k)&=&(399/400)-(1/6)(\sin(28\pi k/5600))^8.\end{array}$

This image shows all circles of the form:
$(x-A(k))^2+(y-B(k))^2=(R(k))^2$, for $k=-10000, -9999, \ldots , 9999, 10000$, where

$\begin{array}{lllcl}A(k)&=&(3k/20{,}000)&+&\sin((\pi /2)(k/10{,}000)^7)((\cos(41\pi k/10{,}000))^6)\\&&&+&(1/4)((\cos(41\pi k/10{,}000))^{16})((\cos(\pi k/20{,}000))^{12})\sin(6\pi k/10{,}000),\end{array}$

$\begin{array}{lll}B(k)&=&-\cos((\pi /2)(k/10{,}000)^7)*\\&&(1+(3/2)(\cos(\pi k/20{,}000)\cos(3\pi k/20{,}000))^6)*\\&&((\cos(41\pi k/10{,}000))^6)+(1/2)(\cos(3\pi k/100{,}000)\cos(9\pi k/100{,}000)\cos(18\pi k/100{,}000))^{10},\end{array}$

$\begin{array}{lllcl}R(k)&=&(1/50)&+&(1/10)((\sin(41\pi k/10{,}000)\sin(9\pi k/100{,}000))^2)\\&&&+&(1/20)((\cos(41\pi k/10{,}000))^2)((\cos(\pi k/20{,}000))^{10}).\end{array}$